Active Flows using Coarse-Grained Numerical Methods
ICMCS, 25th September, 2023
Timofey Kozhukhov (t.kozhukhov@sms.ed.ac.uk), Tyler N. Shendruk (t.shendruk@ed.ac.uk)

View these slides online at www.Kozhukhov.co.uk/

Table of contents
- Introduction & Motivation
- Mesoscopic simulation techniques &
Multi-Particle Collision Dynamics (MPCD) - Active Nematic (AN-) MPCD
- Modulated AN-MPCD
- Applications of AN-MPCD
- Conclusion
Active matter ranges across scales
- Individual "active" units
- Local energy injection from environment
- Energy used to locomote
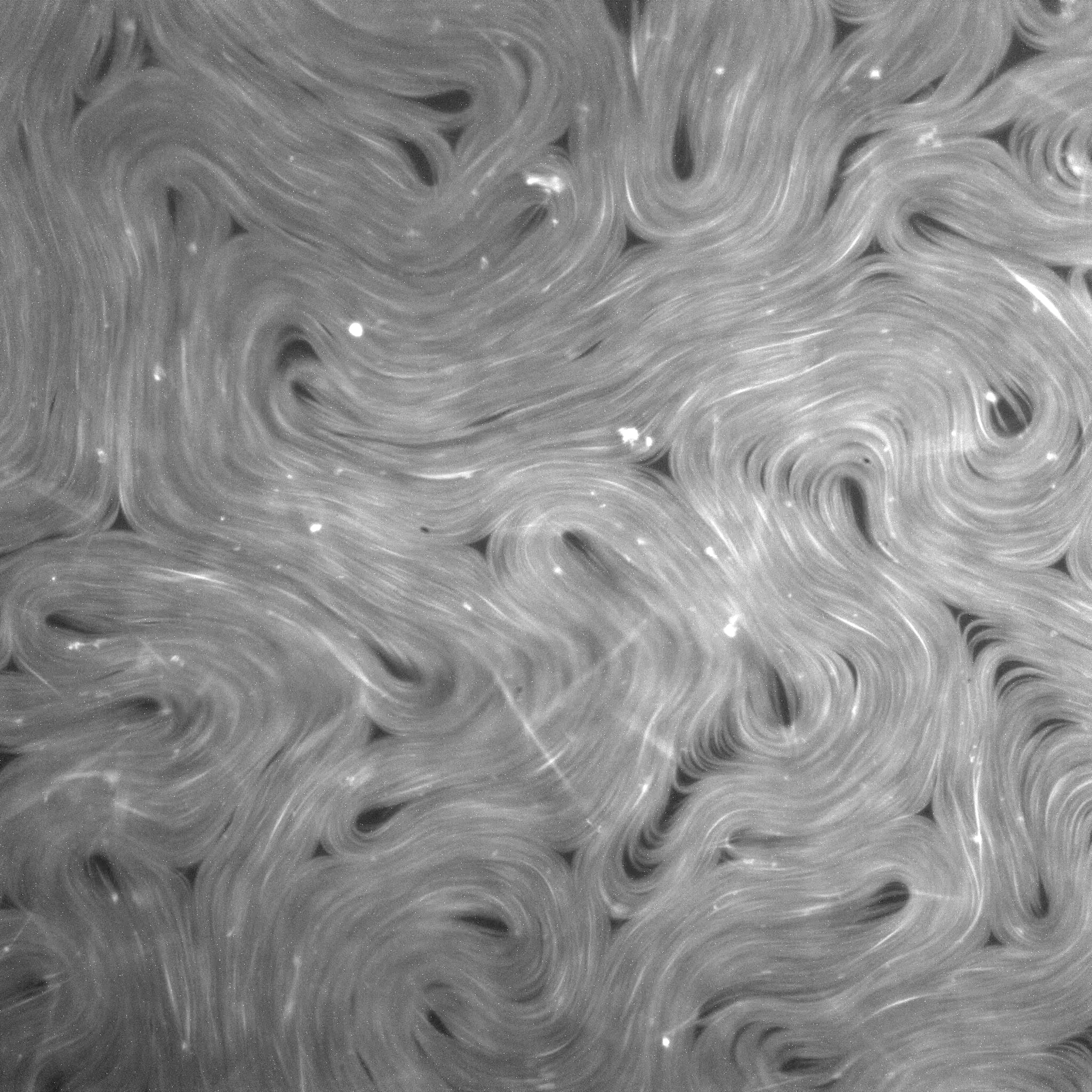
Microtubule bundle systems are active nematics


Active Nematic
Microtubule bundle systems are active nematics




+1/2
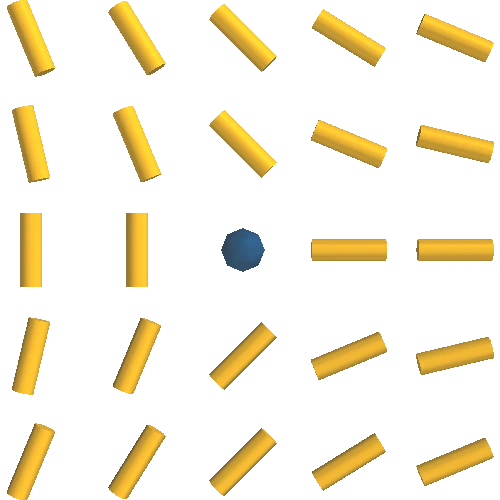
-1/2
Mesoscale active matter has seen rapid recent progress
Table of contents
- Introduction & Motivation
- Mesoscopic simulation techniques &
Multi-Particle Collision Dynamics (MPCD) - Active Nematic (AN-) MPCD
- Modulated AN-MPCD
- Applications of AN-MPCD
- Conclusion
Active matter simulation methods exist across scales
Microscopic
Macroscopic
Mesoscale methods for this subset of active systems are limited
Our requirements:
- Includes hydrodynamic interactions
- Suitable for complex geometries & boundaries
- Moderate Peclet number
- Suitable for wide variety of active systems
MD

MD
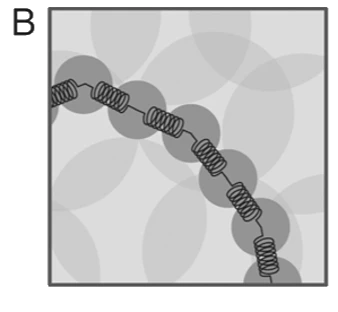
DPD

DPD
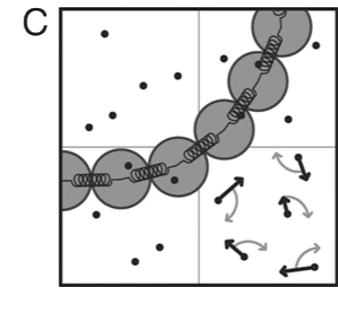
MPCD

MPCD
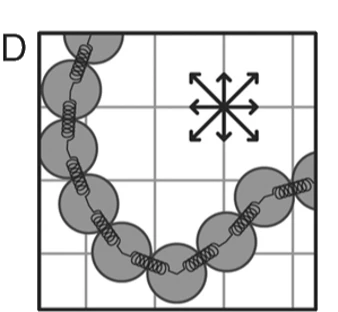
LB

LB
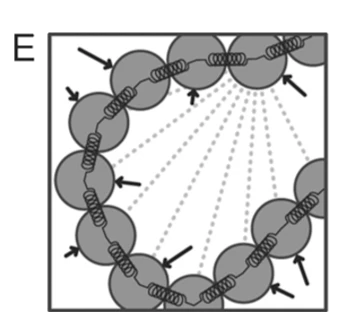
Stokesian Dyn.

Stokesian Dyn.
Langevin Dyn.

Langevin Dyn.
What is Multi-Particle Collision Dynamics (MPCD)?
Particle $i$ has:
Cell $C$ has:
- Position $\vec x_i$
- Velocity $\vec v_i$
- Mass $m_i$
Cell $C$ has:
- Population $\rho_C$
- CoM velocity $\vec v_{CM}$
- Moment of intertia $I_C$

Streaming: $\vec{x}_i(t+\delta t) = \vec{x}_i(t) + \vec{v}_i(t)\delta t$
Collision:
$\vec{v}_i(t+\delta t) = \vec{v}_{CM}(t) + \vec\Xi_i(\vec{r}_\mathrm{CM}, t)$
$\vec{v}_i(t+\delta t) = \vec{v}_{CM}(t) + \textcolor{crimson}{\vec\Xi_i(\vec{r}_\mathrm{CM}, t)}$
The collision operator controls the material properties
A collision operator $\textcolor{crimson}{\vec \Xi_C}$ acting on cell $C$ must:
- Include some stochasticity
- Respect conservation laws (linear momentum, etc)
- Exchange particle properties (velocities, etc)
Angular momentum conserving Andersen collision operator:
$ \color{crimson}{\Xi_i^{A}} $ $ = \color{cerulean}\underline{\color{black}\vec\xi_i(t) } $ $ - \color{crimson}\underline{\color{black}\langle \vec\xi\rangle_{N_C} } $ $ + \color{amber}\underline{\color{black}{(I_C^{-1}\cdot \delta L_C ) \times \vec{r}_i}} $
where $\delta L_C$ is the angular momentum change
$ \color{crimson}{\Xi_i^{A}} $ $ = \color{cerulean}\underline{\color{black}\vec\xi_i(t) } $ $ - \color{crimson}\underline{\color{black}\langle \vec\xi\rangle_{N_C} } $ $ + \color{amber}\underline{\color{black}{(I_C^{-1}\cdot \delta L_C ) \times \vec{r}_i}} $
where $\delta L_C$ is the angular momentum change

François de Tournemire
Modifying collision operators simulates new materials
Particle $i$ has:
Cell $C$ has:
- Position $\vec x_i$
- Velocity $\vec v_i$
- Mass $m_i$
- Orientation $\vec u_i$
Cell $C$ has:
- Population $\rho_C$
- CoM velocity $\vec v_{CM}$
- Moment of inertia $I_C$
- Local director $\vec n_C$
Velocity collision: $\vec{v}_i(t+\delta t) = \vec{v}_{CM}(t) + \textcolor{crimson}{\vec\Xi_i(\vec{r}_\mathrm{CM}, t)}$
Orientation collision: $\vec{u}_i(t+\delta t) = \vec{n}_C(t) + \textcolor{cerulean}{\vec{\eta}_i(t)}$
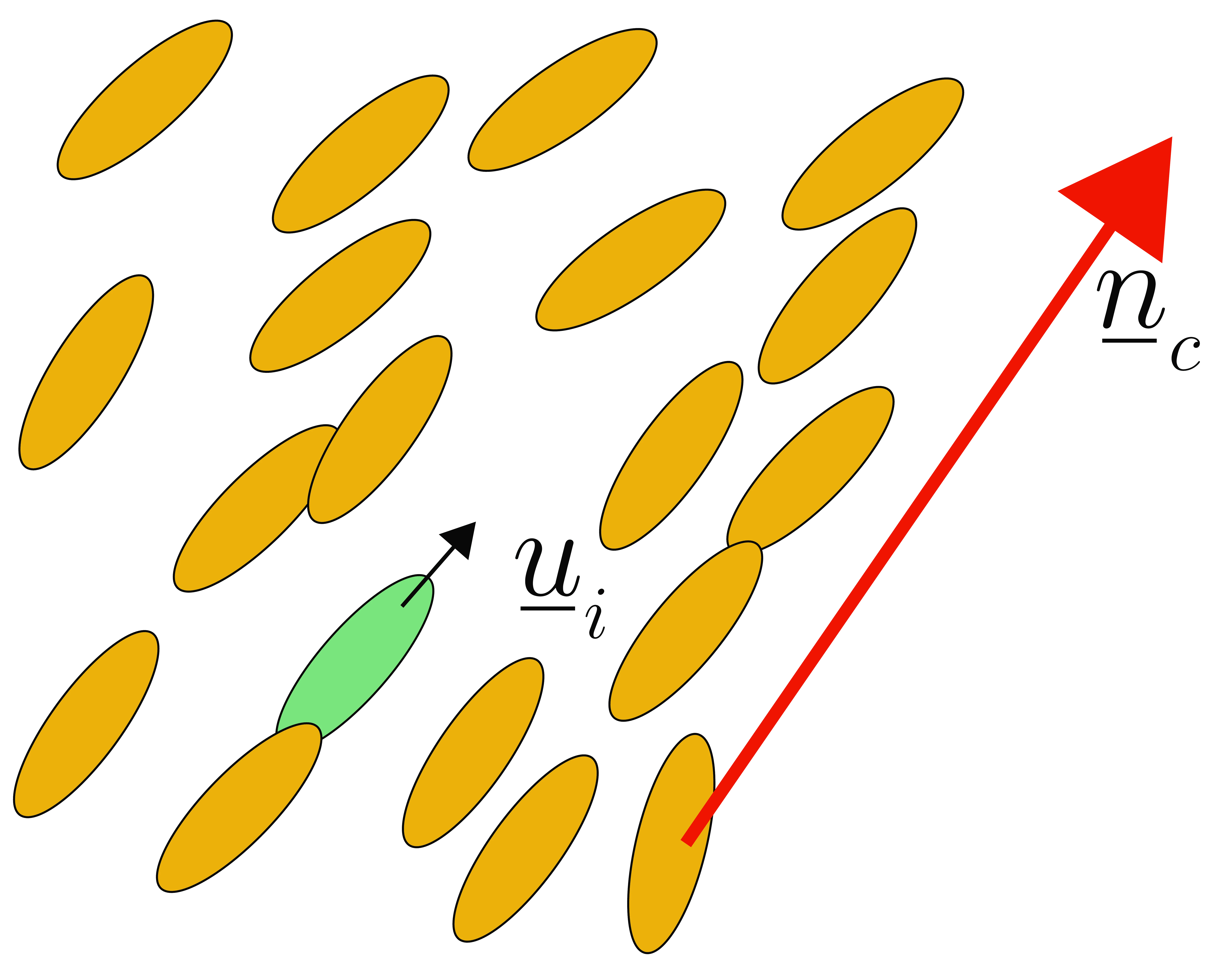
$\textcolor{cerulean}{\vec{\eta}_i}$ orientation drawn from a Maier-Saupe distribution \[ \begin{align*} \textcolor{crimson}{\Xi_i^{N}} &= \textcolor{crimson}{\Xi_i^{A}} + (I_C^{-1}\cdot \delta \mathcal{L}_C) \times \vec{r}_i \end{align*} \]
Orientation collision: $\vec{u}_i(t+\delta t) = \vec{n}_C(t) + \textcolor{cerulean}{\vec{\eta}_i(t)}$

$\textcolor{cerulean}{\vec{\eta}_i}$ orientation drawn from a Maier-Saupe distribution \[ \begin{align*} \textcolor{crimson}{\Xi_i^{N}} &= \textcolor{crimson}{\Xi_i^{A}} + (I_C^{-1}\cdot \delta \mathcal{L}_C) \times \vec{r}_i \end{align*} \]
- Shendruk T, Yeomans J, Soft Matter 2015
Simple changes to collision operators give nematic behaviour
- Shendruk T, Yeomans J, Soft Matter 2015
Table of contents
- Introduction & Motivation
- Mesoscopic simulation techniques &
Multi-Particle Collision Dynamics (MPCD) - Active Nematic (AN-) MPCD
- Modulated AN-MPCD
- Applications of AN-MPCD
- Conclusion
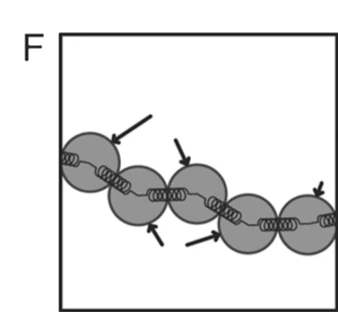
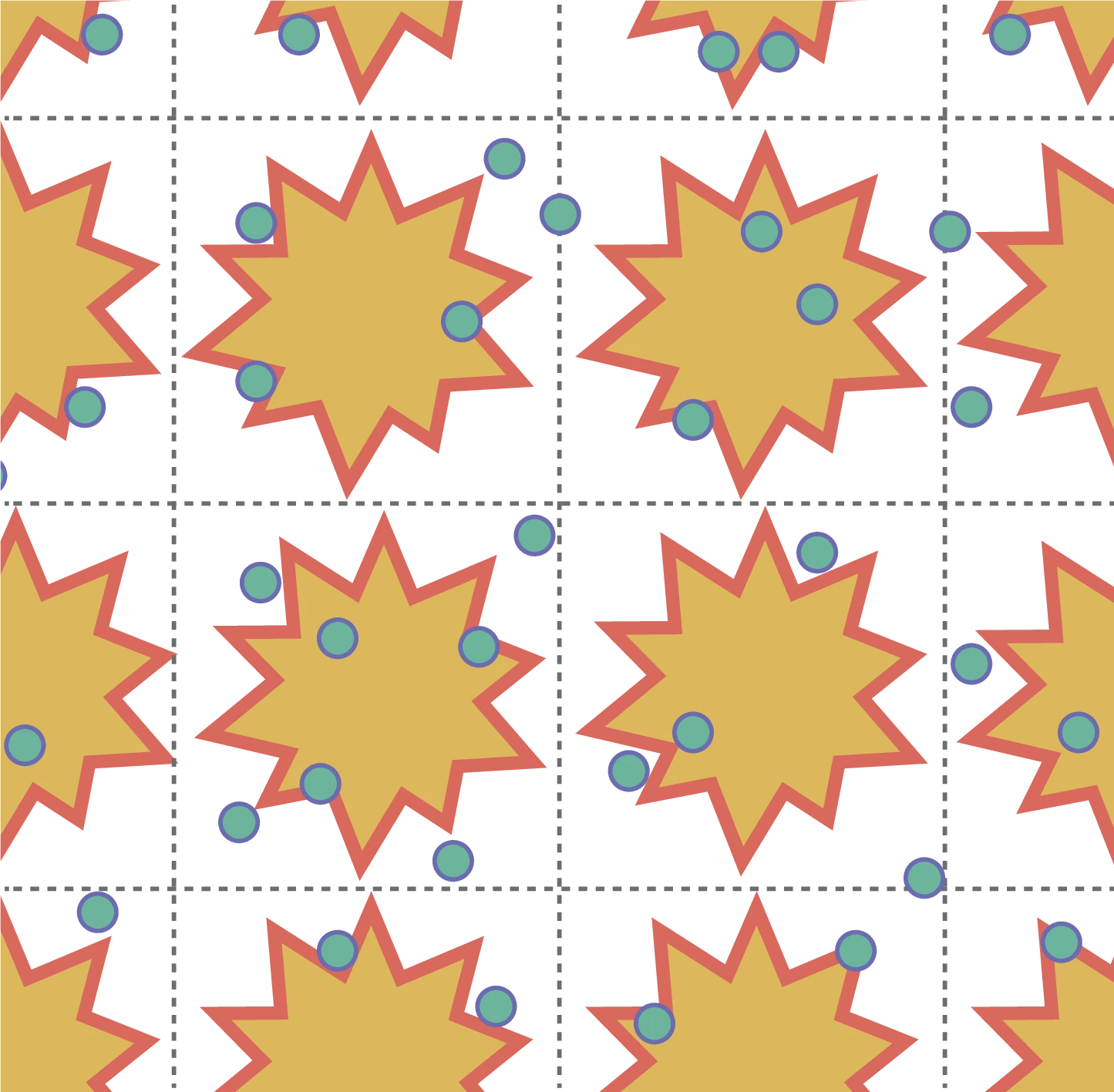
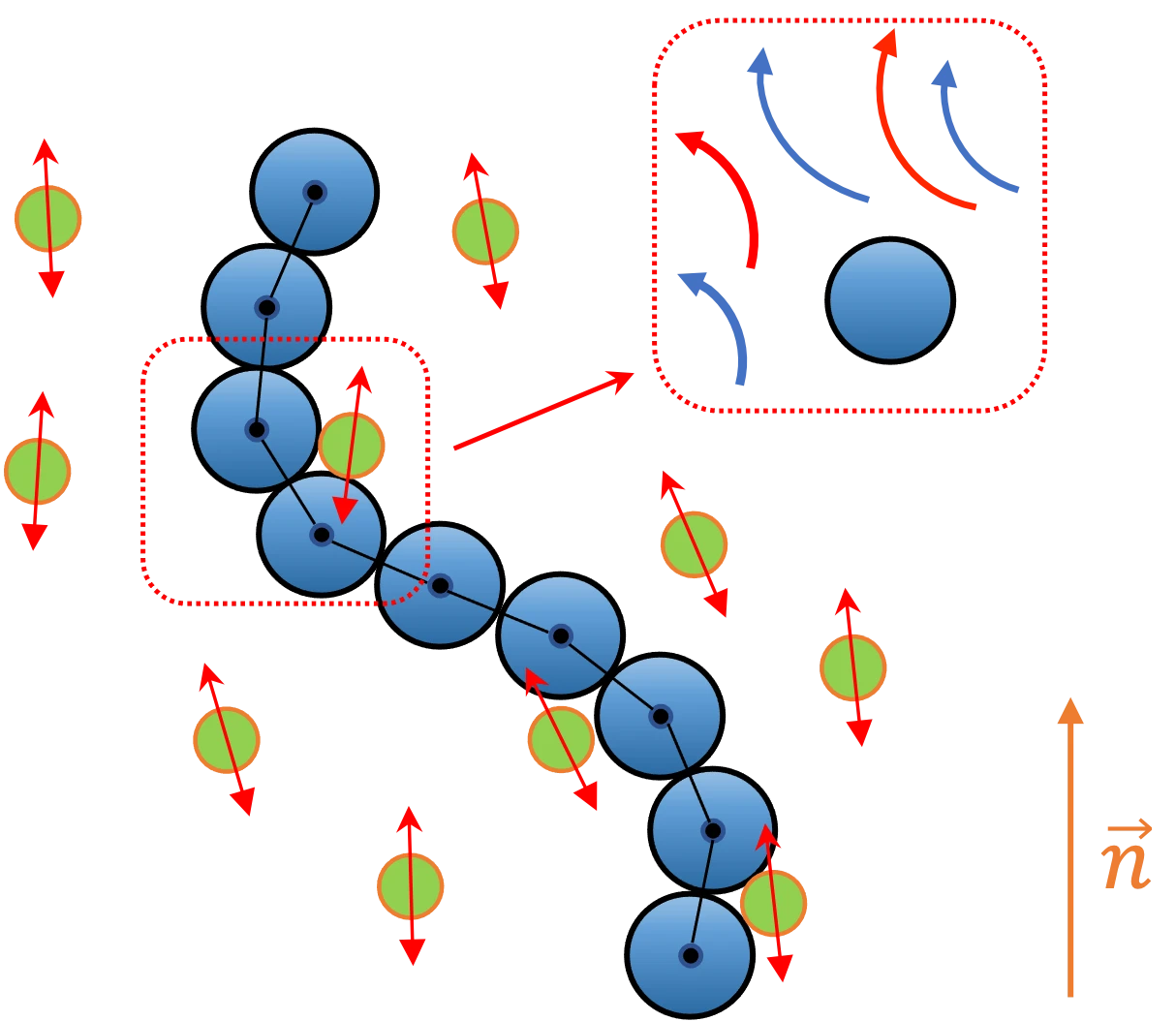
Local force dipoles are necessary for an active-nematic


A planar collision rule induces local force dipoles
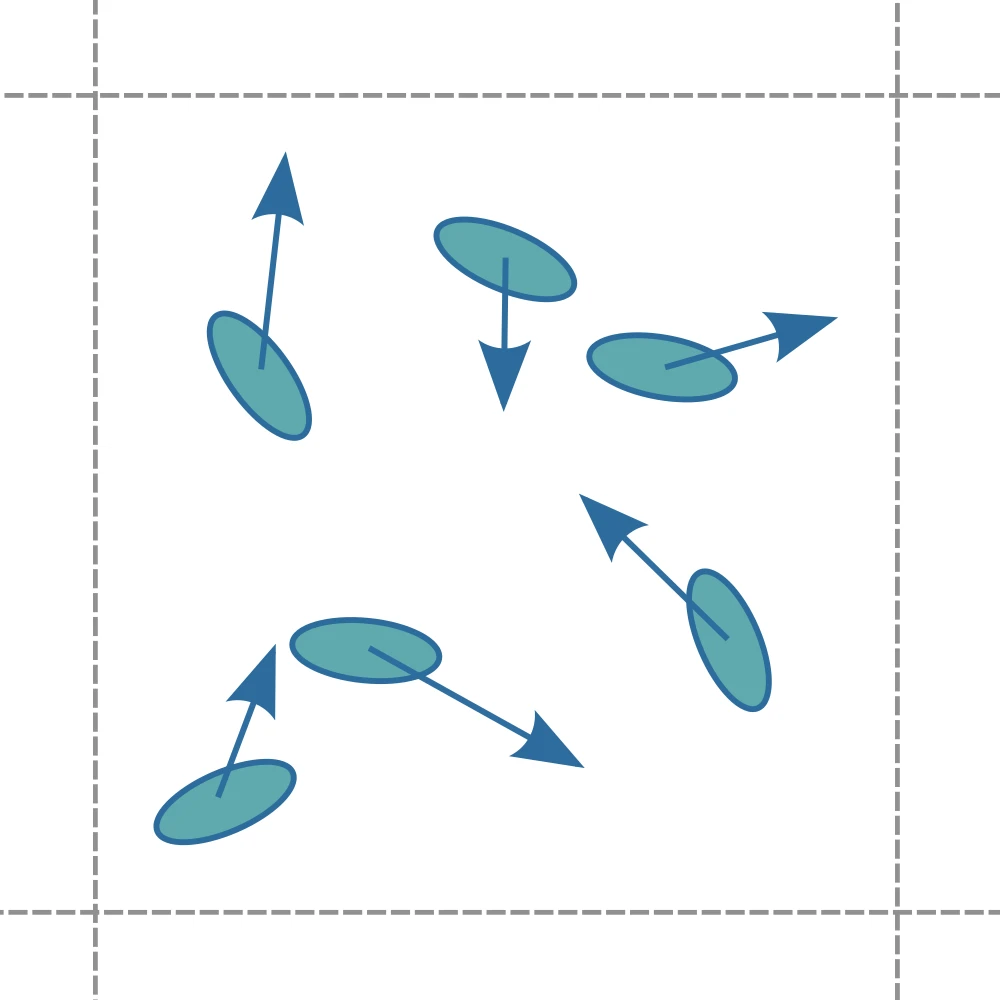
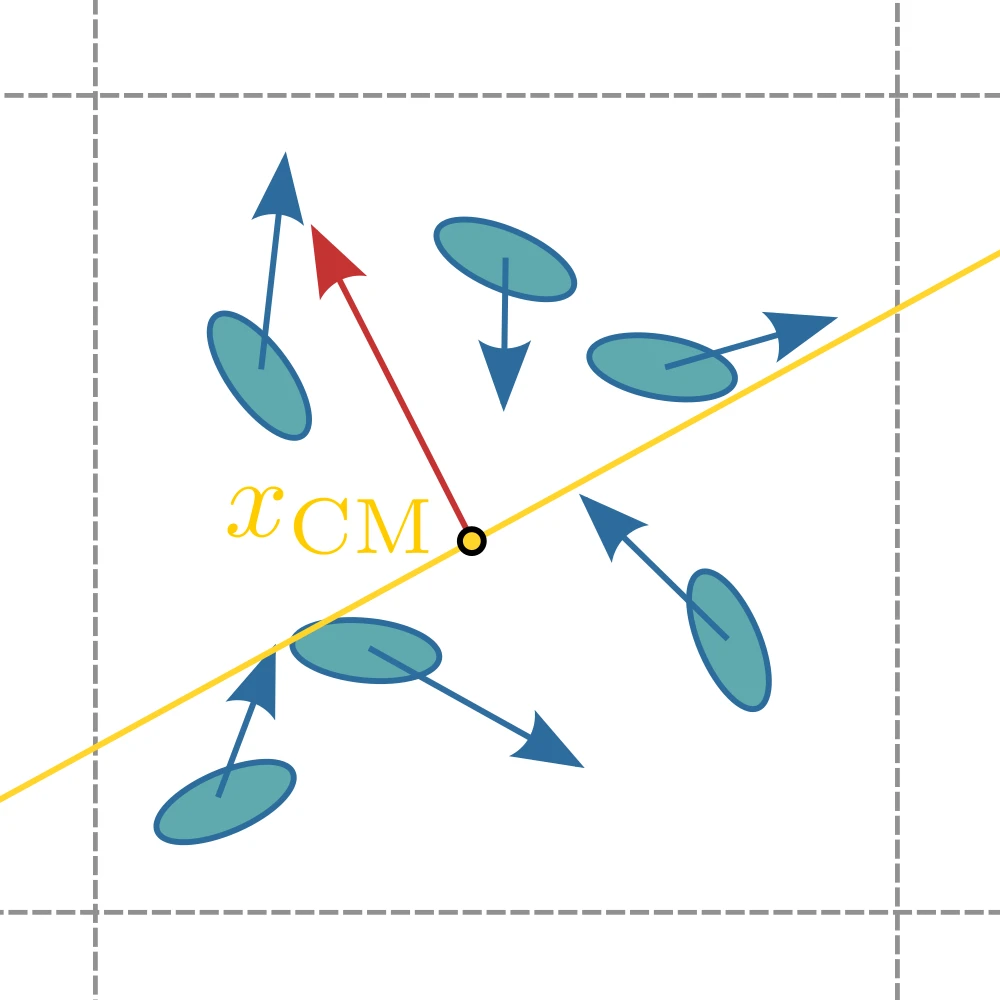
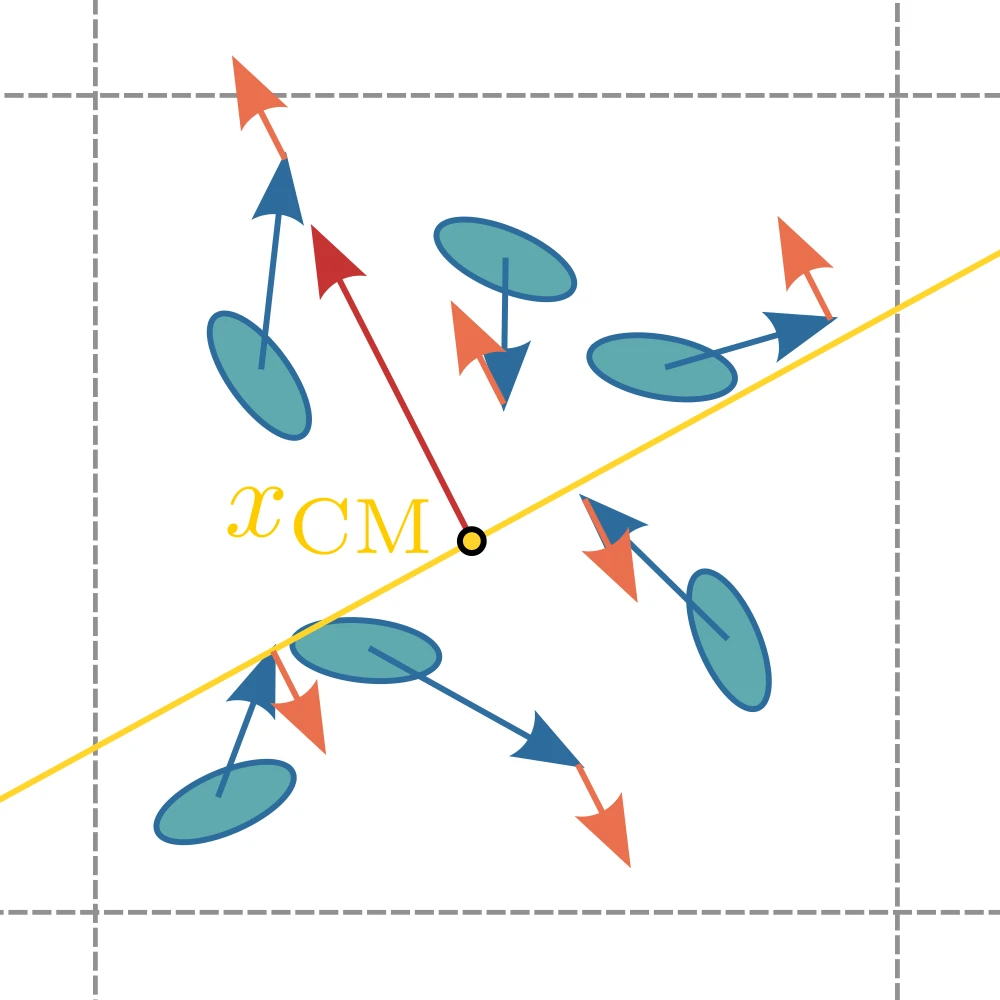
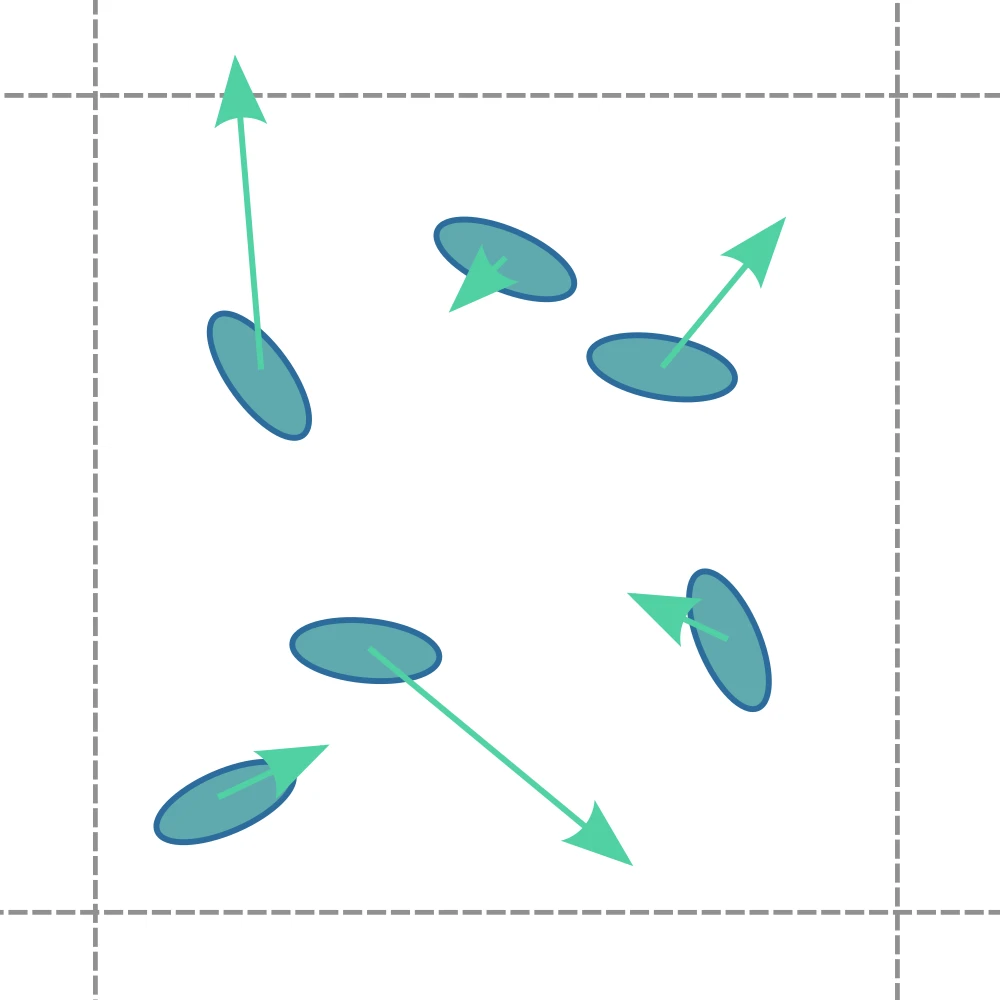
Cellular activity $\alpha_C$ - Local force magnitude
- Kozhukhov T, Shendruk T, Sci. Adv., 2022
Activity magnitude changes algorithm regime
$\alpha < \alpha_\text{eq} = 10^{-3}$
$10^{-3} = \alpha_\text{eq} < \alpha < \alpha_\text{turb} = 2.5\times 10^{-2}$
$\alpha > \alpha_\text{turb} = 2.5\times 10^{-2}$
- Kozhukhov T, Shendruk T, Sci. Adv., 2022
Active-Nematic (AN-) MPCD Reproduces Active Turbulence
- Kozhukhov T, Shendruk T, Sci. Adv., 2022
AN-MPCD turbulence begins from high bend walls
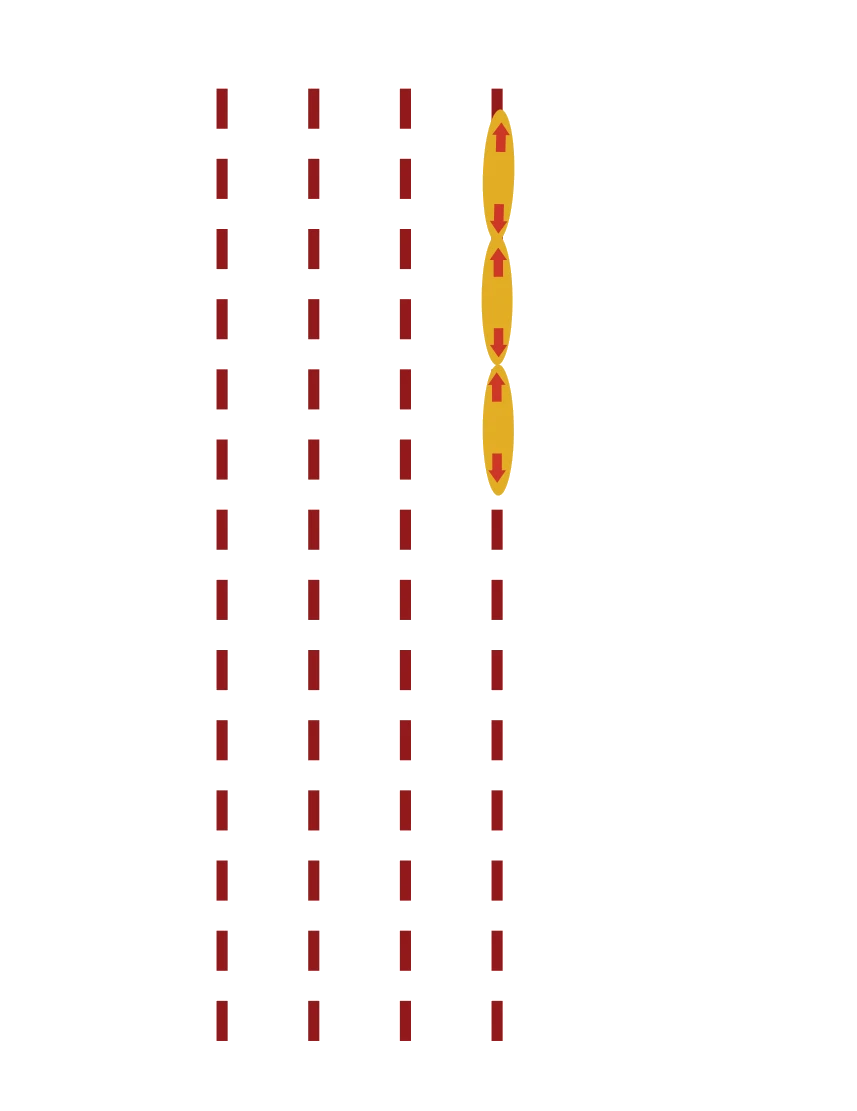
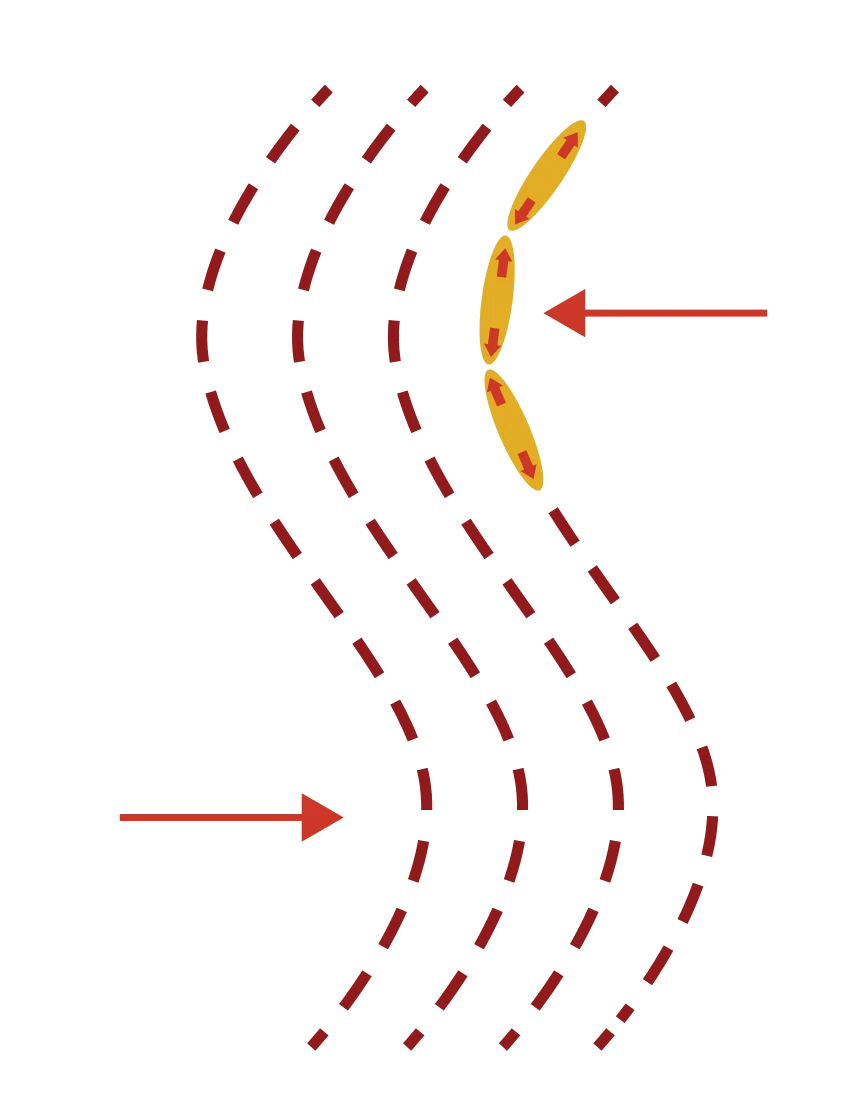

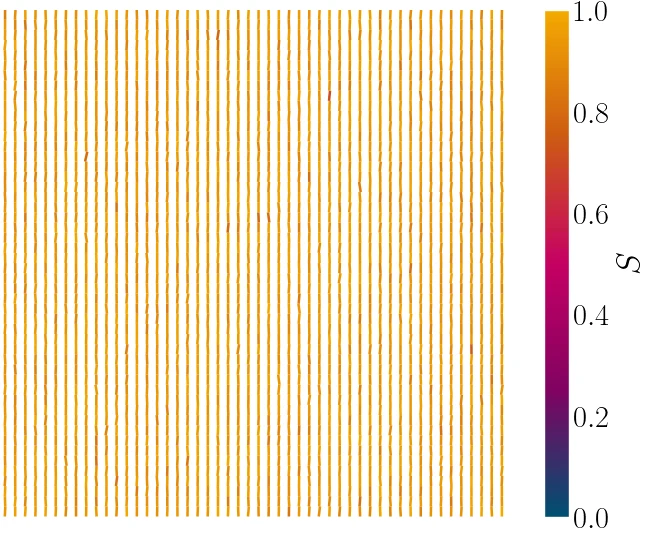


AN-MPCD succesfully reproduces active turbulence
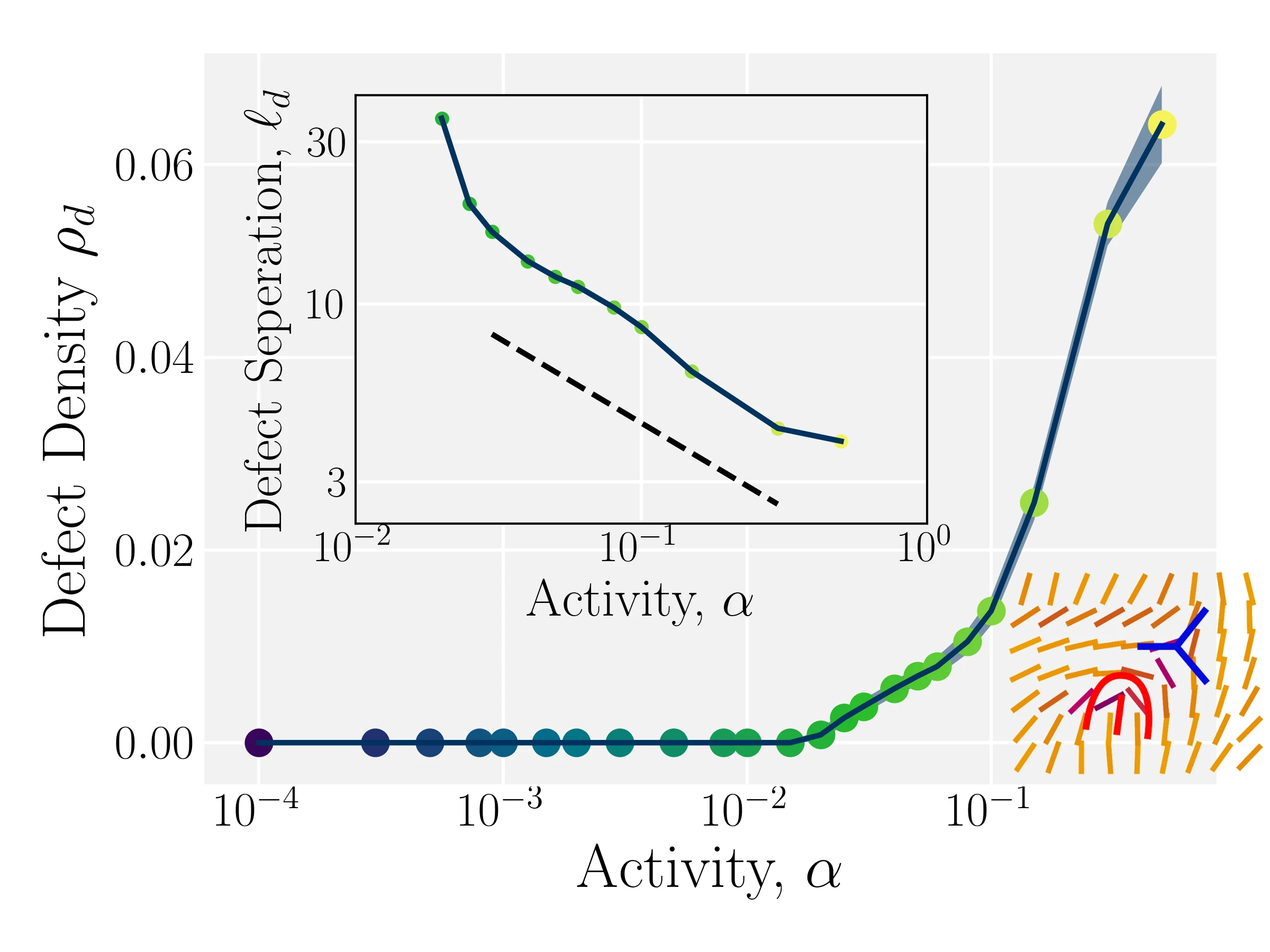
$\ell_d = \rho_d^{-1/2}$; Theory: $\ell_d \propto \alpha^{-1/2}$
AvLL_scale-web.webp)
Theory: $v \propto \alpha^{1/2}$
- Kozhukhov T, Shendruk T, Sci. Adv., 2022
Active particle model results in density fluctuations
- Kozhukhov T, Shendruk T, Sci. Adv., 2022
Activity accumulates particles and widens distributions
_ProbDist-web.webp)
_SD_inset-web.webp)
_NoPop-web.webp)
_Quantile-web.webp)
- Kozhukhov T, Shendruk T, Sci. Adv., 2022
Increased activity results in giant number fluctuations
Central Limit Theorem: $\sigma_{N_C}\propto \langle N_C \rangle^{1/2}$
_scalesCB-web.webp)
_Gradient-web.webp)
- Kozhukhov T, Shendruk T, Sci. Adv., 2022
Summary on AN-MPCD
- A simple planar collision rule applies a force dipole
- Built-in thermostat sets a minimum activity for turbulence
-
Within the turbulence regime, active turbulence scales per theoretical expectations
- $\alpha > \alpha_\text{turb} = 2.5\times 10^{-2}$
- However has large density fluctuations, common to active particle models
- This is problematic for simulation of solutes
Table of contents
- Introduction & Motivation
- Mesoscopic simulation techniques &
Multi-Particle Collision Dynamics (MPCD) - Active Nematic (AN-) MPCD
- Modulated AN-MPCD
- Applications of AN-MPCD
- Conclusion
Strategy: Modulate local activity
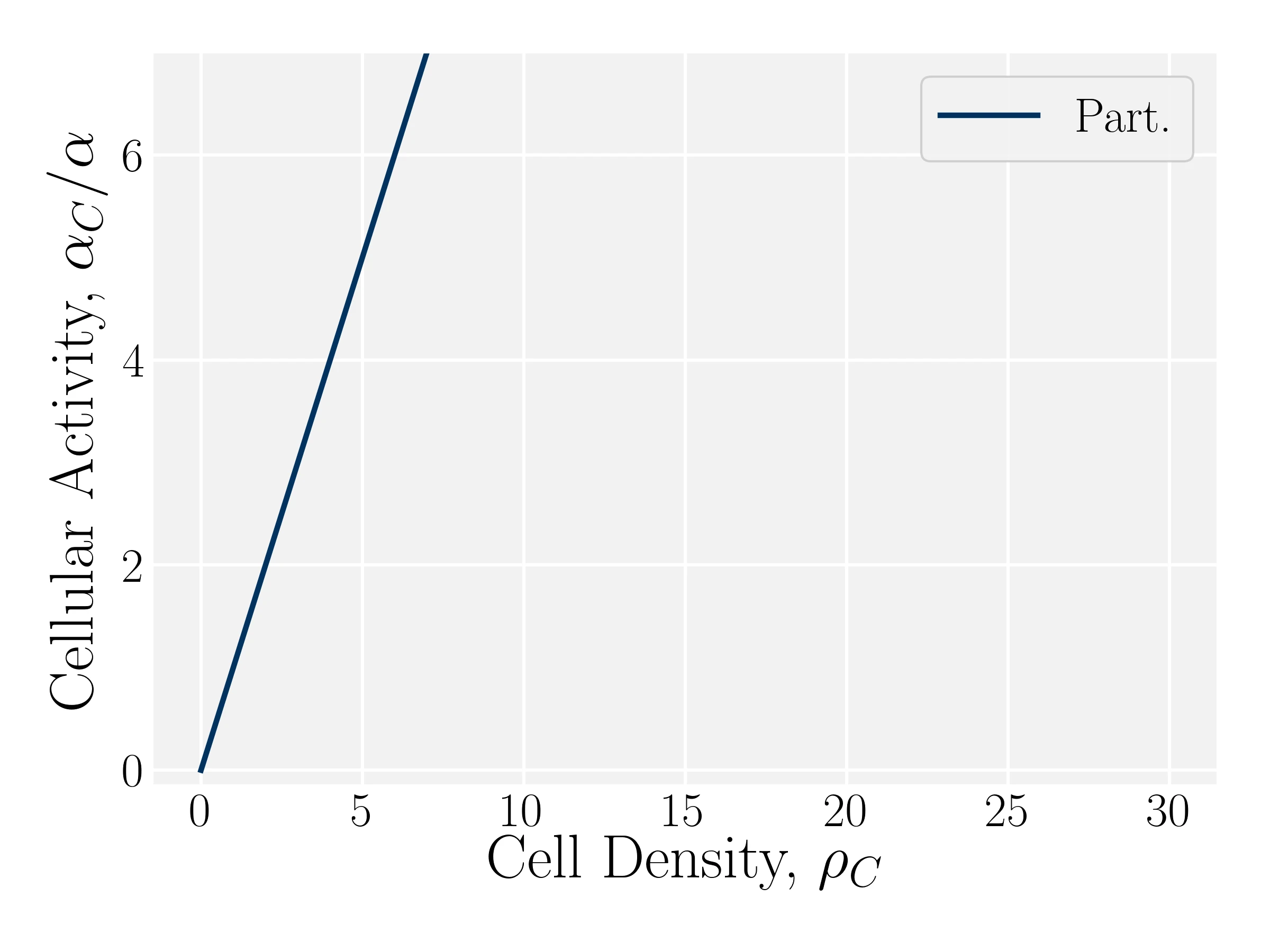
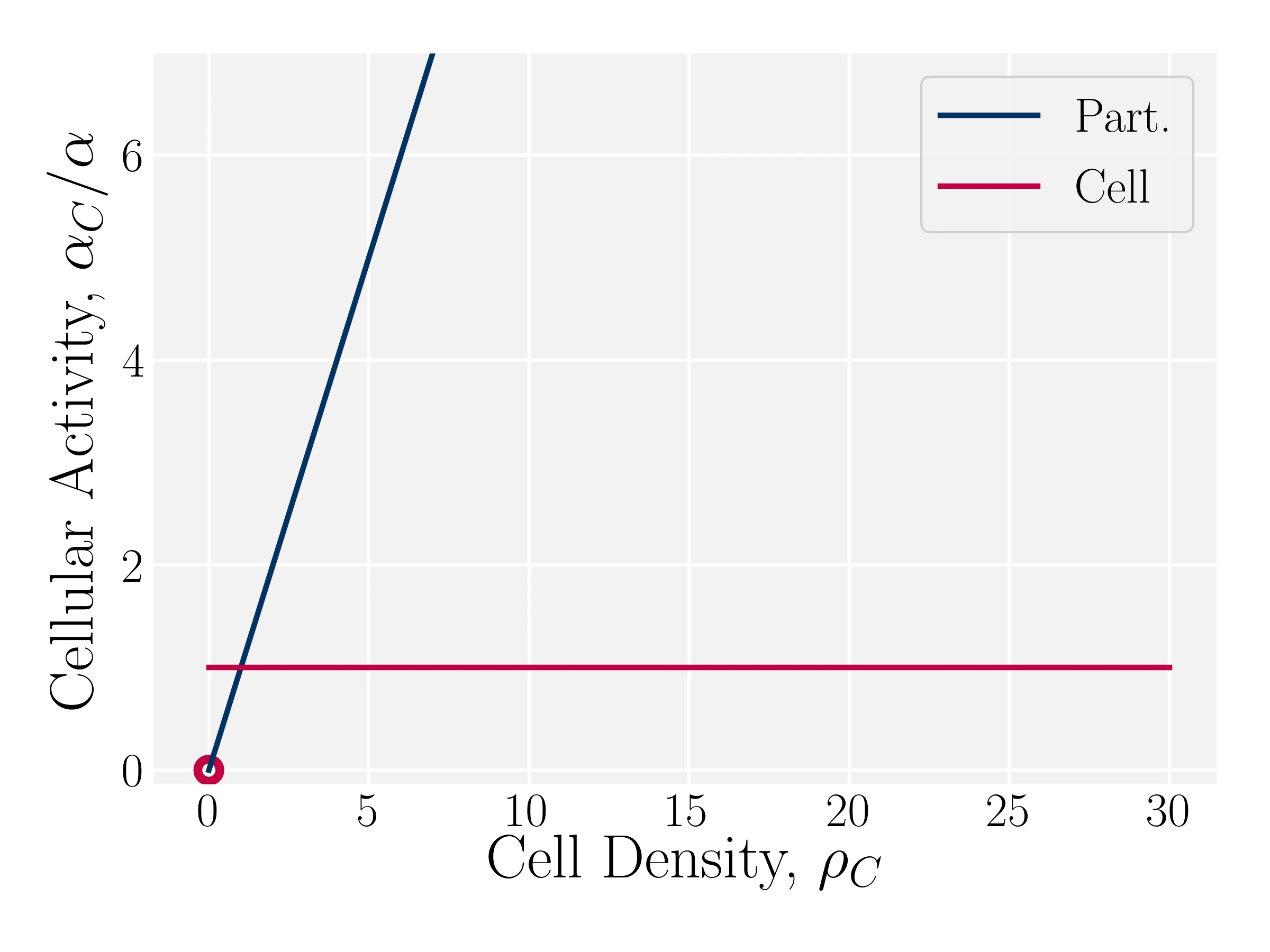
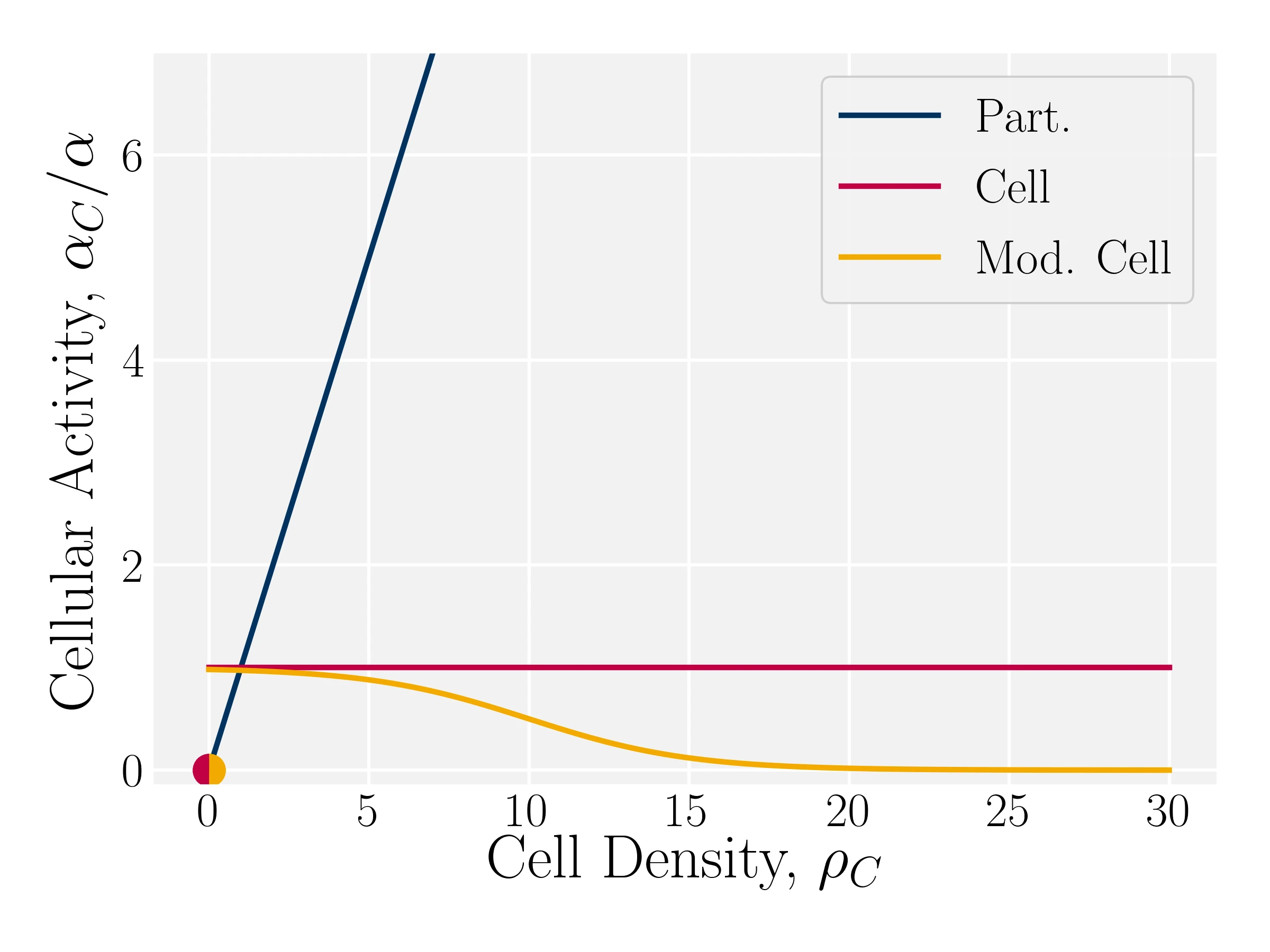
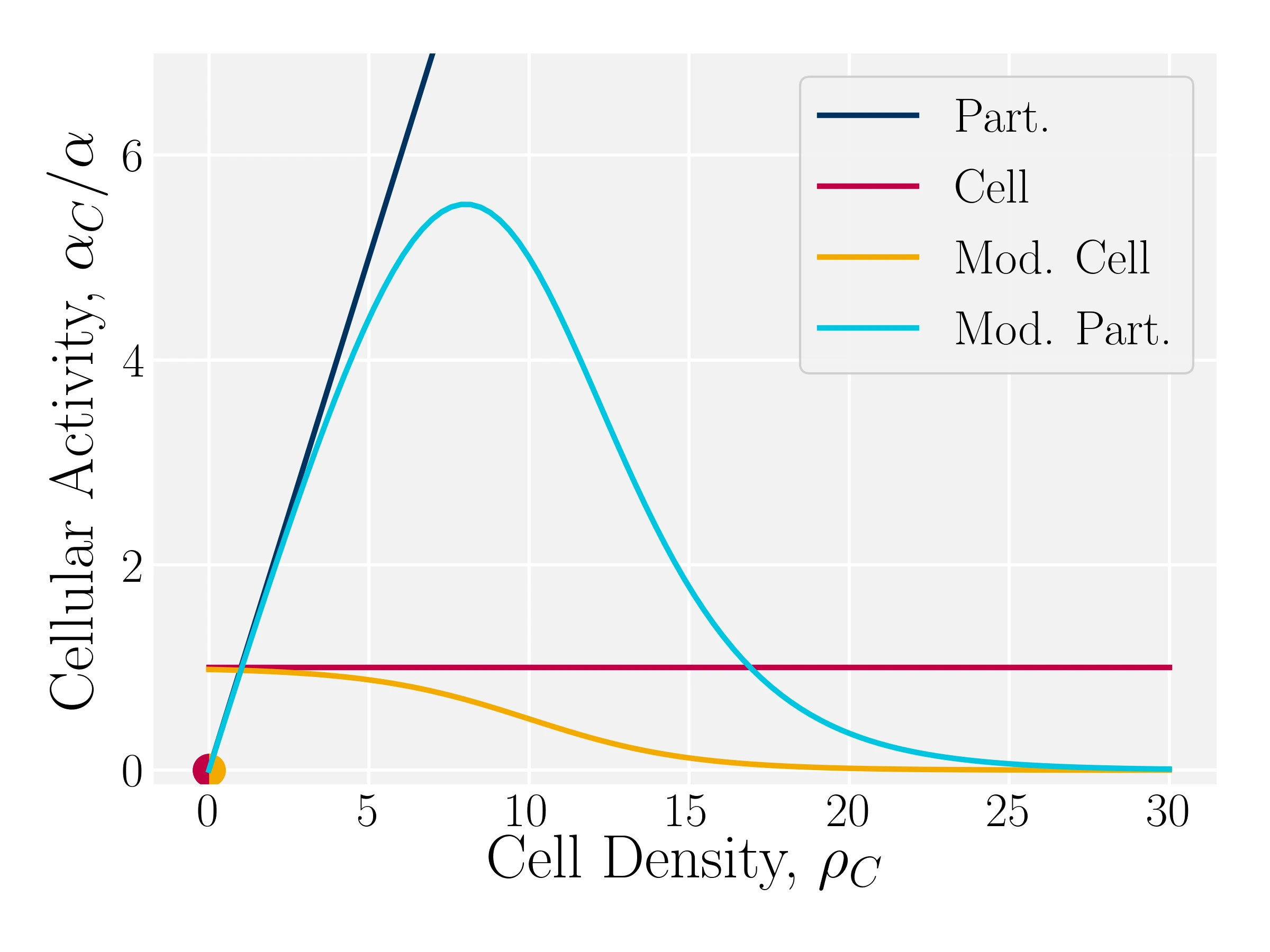
$\Xi_i^{Active} = \Xi_i^{N}+ {\alpha_C} \delta t \left( \frac{\kappa_i}{m_i} - \langle \frac{\kappa_j}{m_j} \rangle_C \right) \vec{n}_C $
- Active Sum (Original): $\alpha_C^\mathrm{S} = \alpha \rho_C$
- Active Average: $\alpha_C^\mathrm{A} = \alpha$
- $\mathcal{S}_C(\rho_C; \sigma_p, \sigma_w) = \frac{1}{2} \left( 1 - \tanh \left( \frac{\rho_C - \av{\rho_C} \left( 1 + \sigma_p \right)}{\av{\rho_C} \sigma_w} \right) \right)$
- Sigmoidal Av.: $\alpha_C^\mathrm{S-A}(\rho_C) = \alpha_C^\mathrm{A} \mathcal{S}_C(\rho_C)$
- Sigmoidal Sum: $\alpha_C^\mathrm{S-S}(\rho_C) = \alpha_C^\mathrm{S} \mathcal{S}_C(\rho_C)$
- Kozhukhov T, Shendruk T, Sci. Adv., 2022
- Kozhukhov T, Loewe B, Shendruk T, in prep.
- Kozhukhov T, Loewe B, Shendruk T, in prep.
- Kozhukhov T, Loewe B, Shendruk T, in prep.
Modulation results in energy input fluctuations
- Active Sum: $\alpha_C^\mathrm{S} = \alpha \rho_C$
- Active Average: $\alpha_C^\mathrm{A} = \alpha$
- Sigmoidal Sum: $\alpha_C^\mathrm{S-S}(\rho_C) = \alpha_C^\mathrm{S} \mathcal{S}_C(\rho_C)$
- Sigmoidal Av.: $\alpha_C^\mathrm{S-A}(\rho_C) = \alpha_C^\mathrm{A} \mathcal{S}_C(\rho_C)$
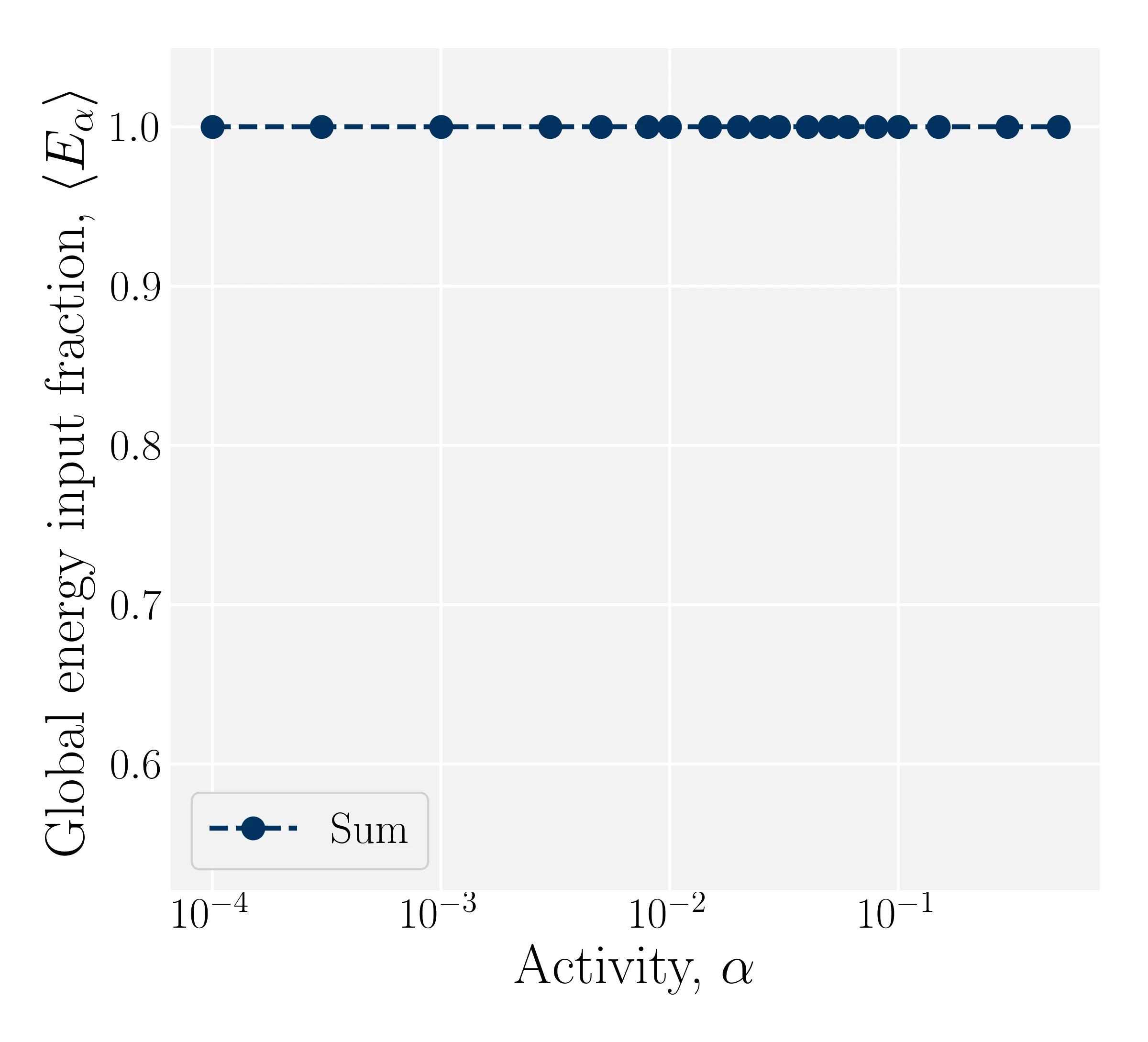
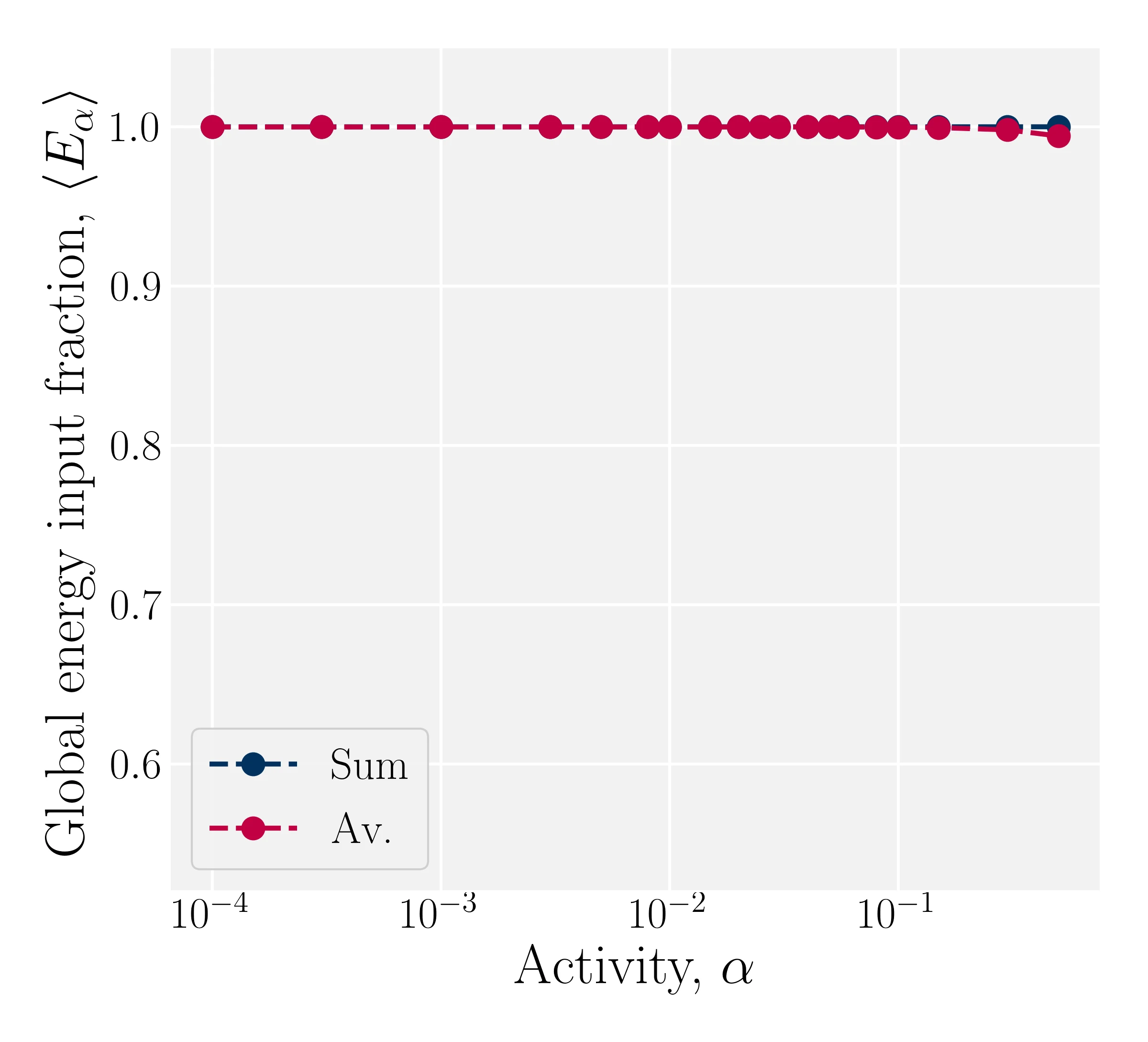
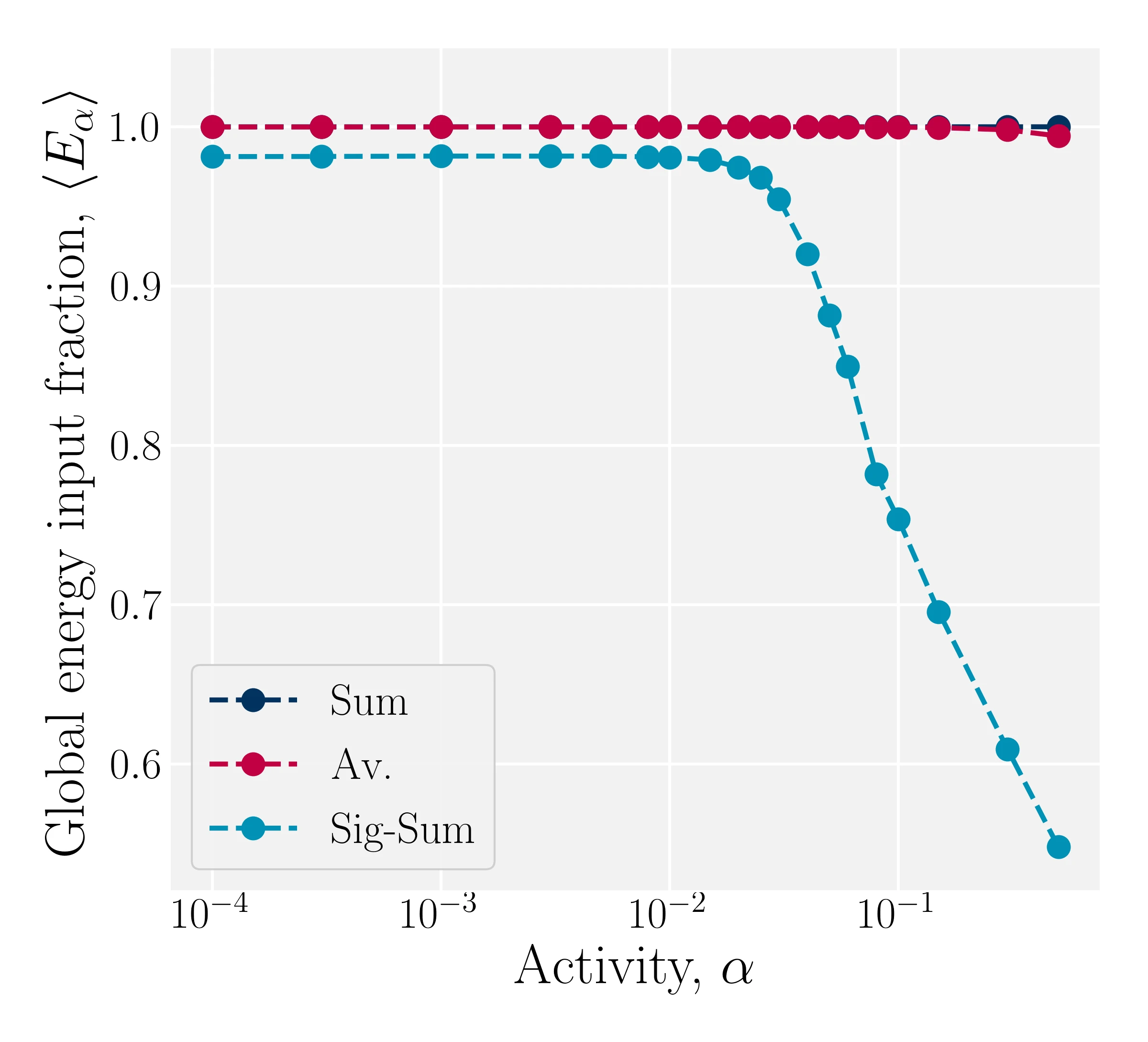
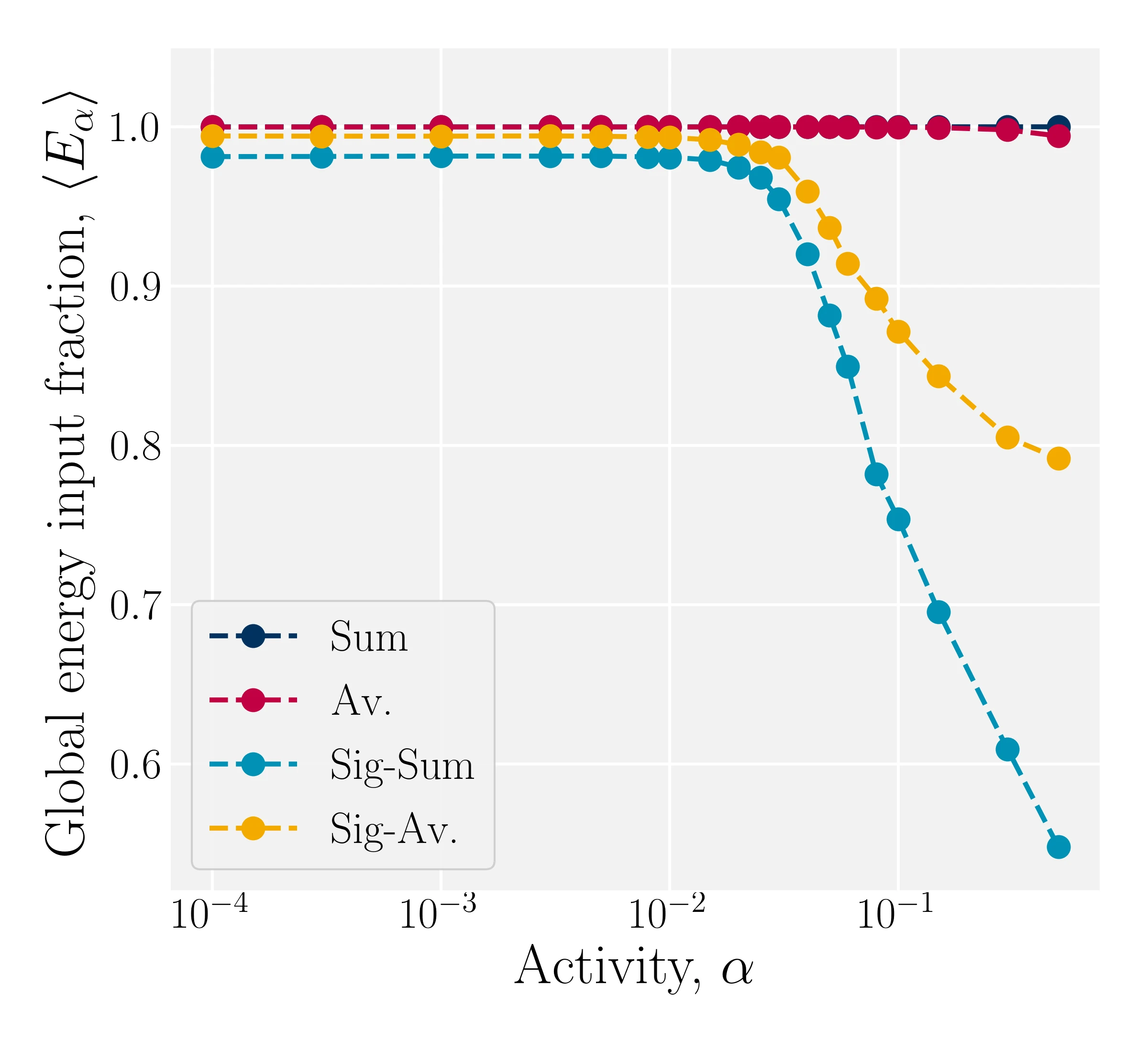
- Kozhukhov T, Loewe B, Shendruk T, in prep.
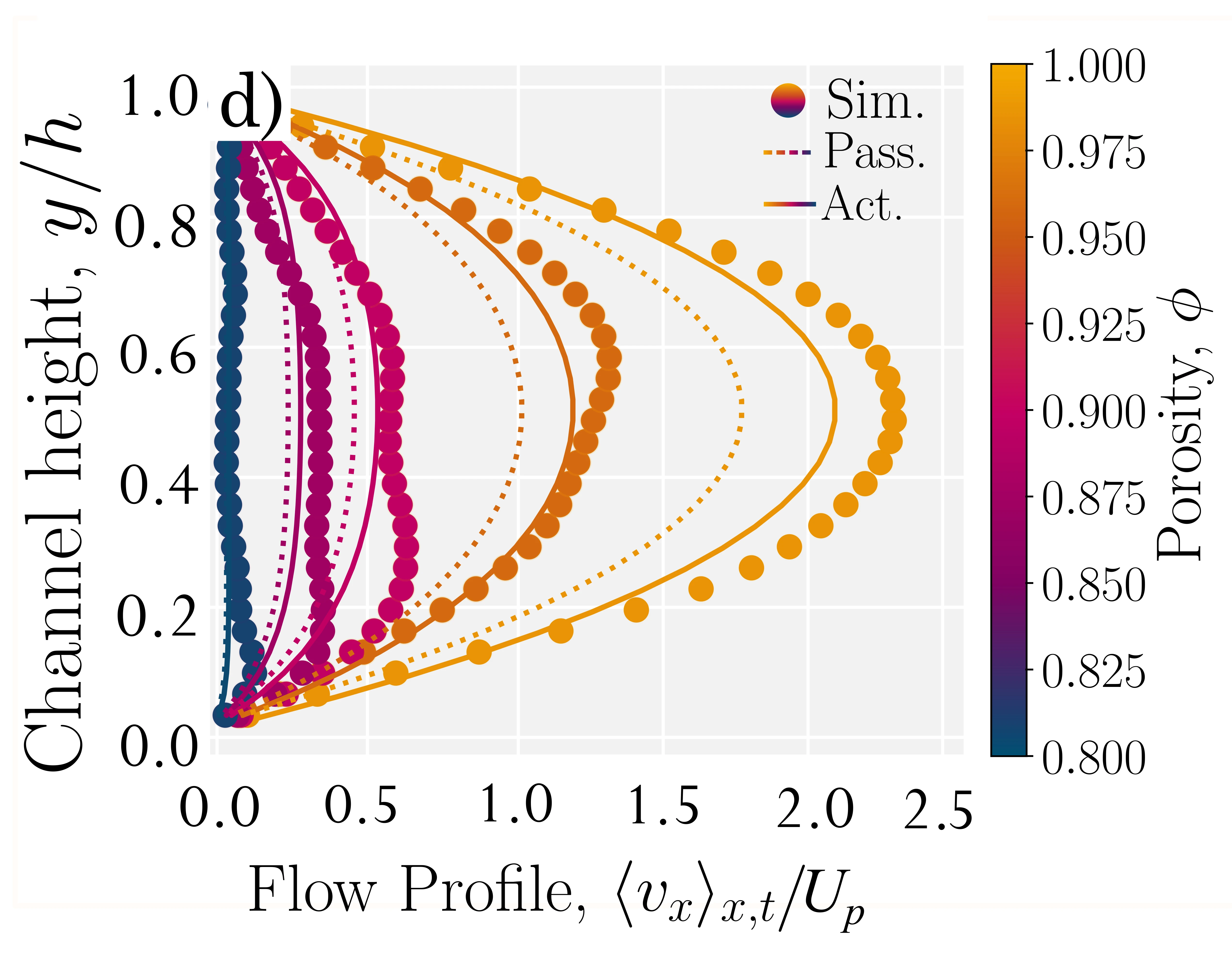
Modulated AN-MPCD reproduces active turbulence
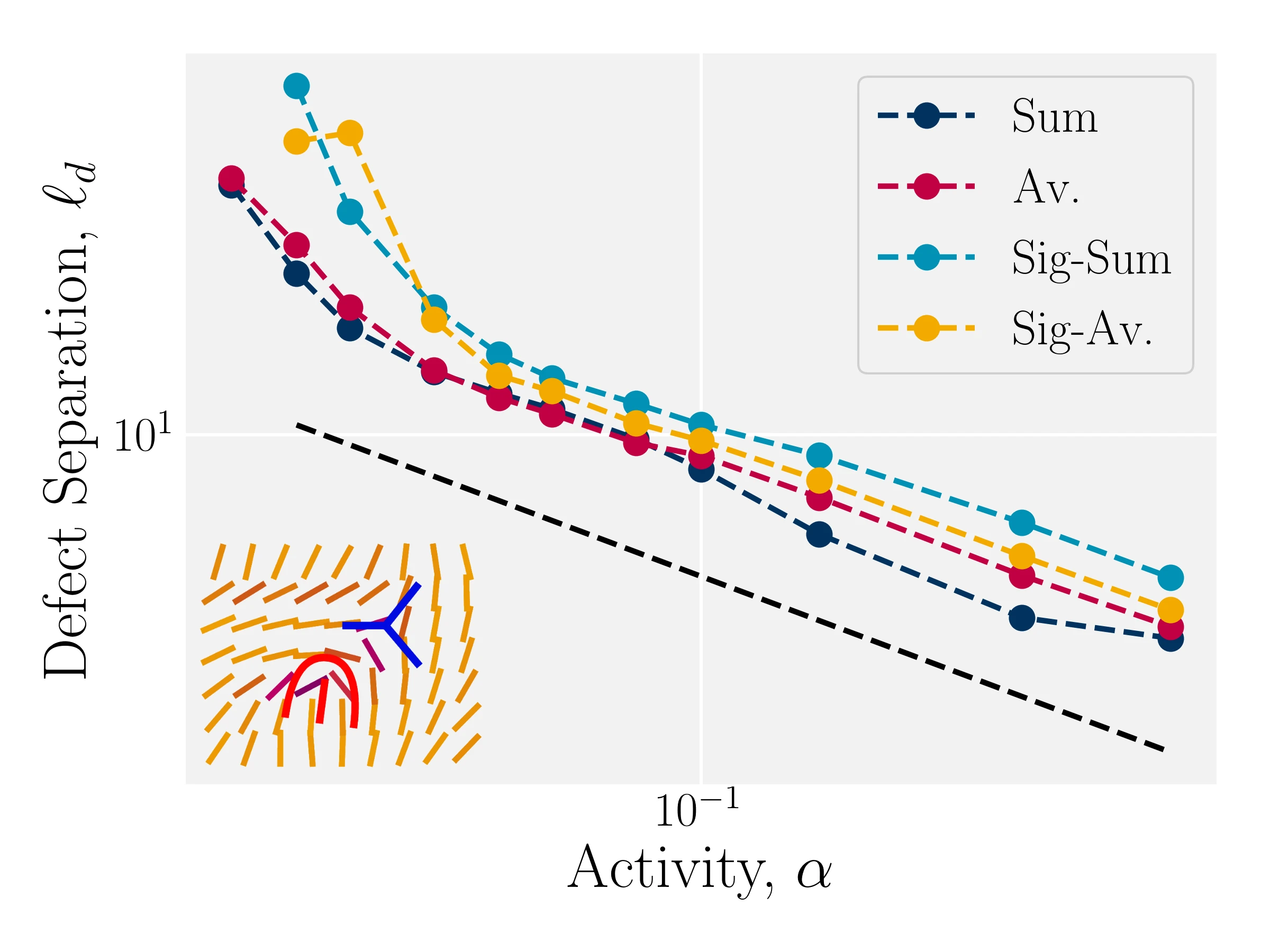
$\ell_d = \rho_d^{-1/2}$; Theory: $\ell_d \propto \alpha^{-1/2}$
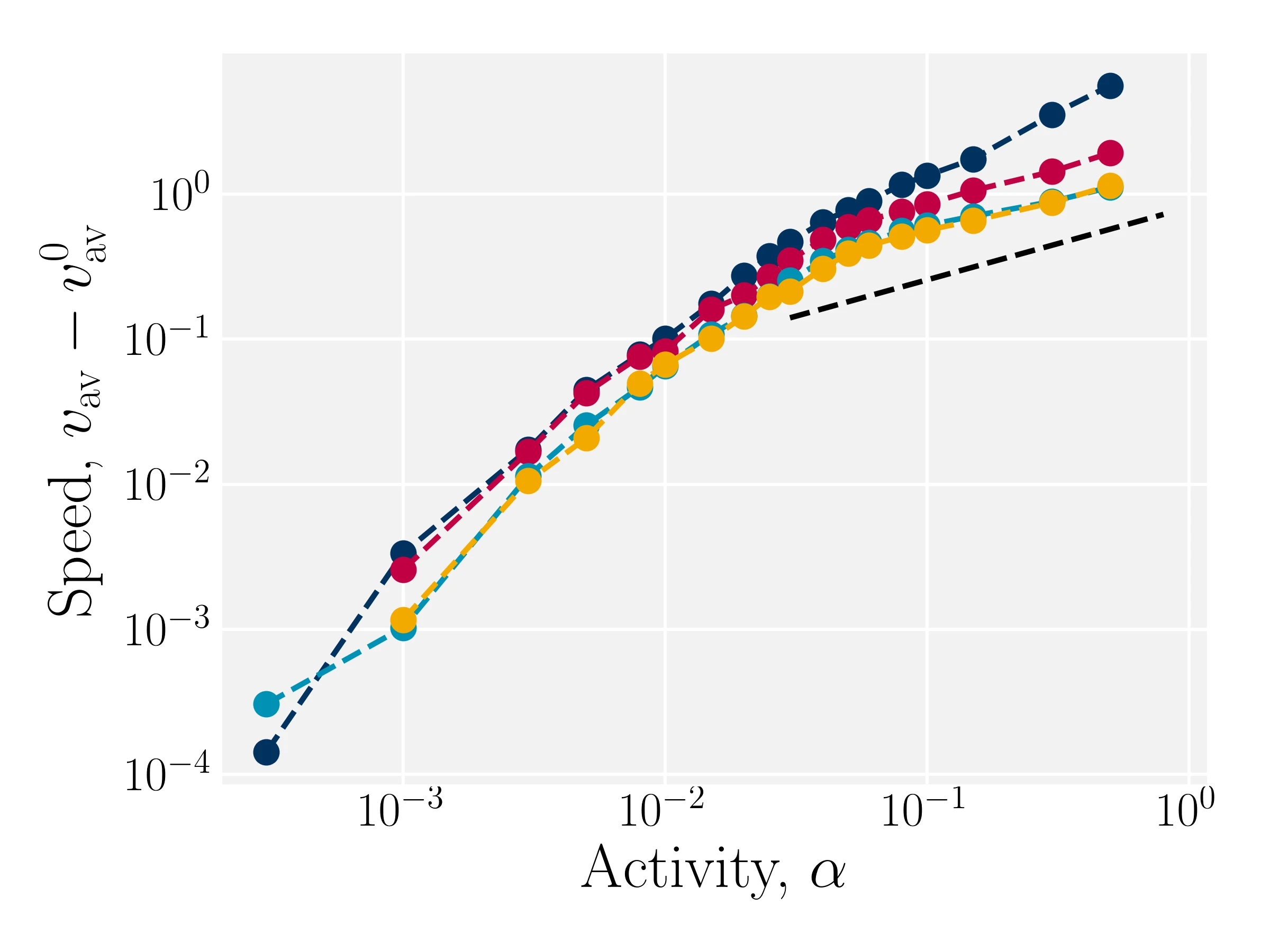
Theory: $v \propto \alpha^{1/2}$
- Kozhukhov T, Loewe B, Shendruk T, in prep.
Modulation results in improved density distributions
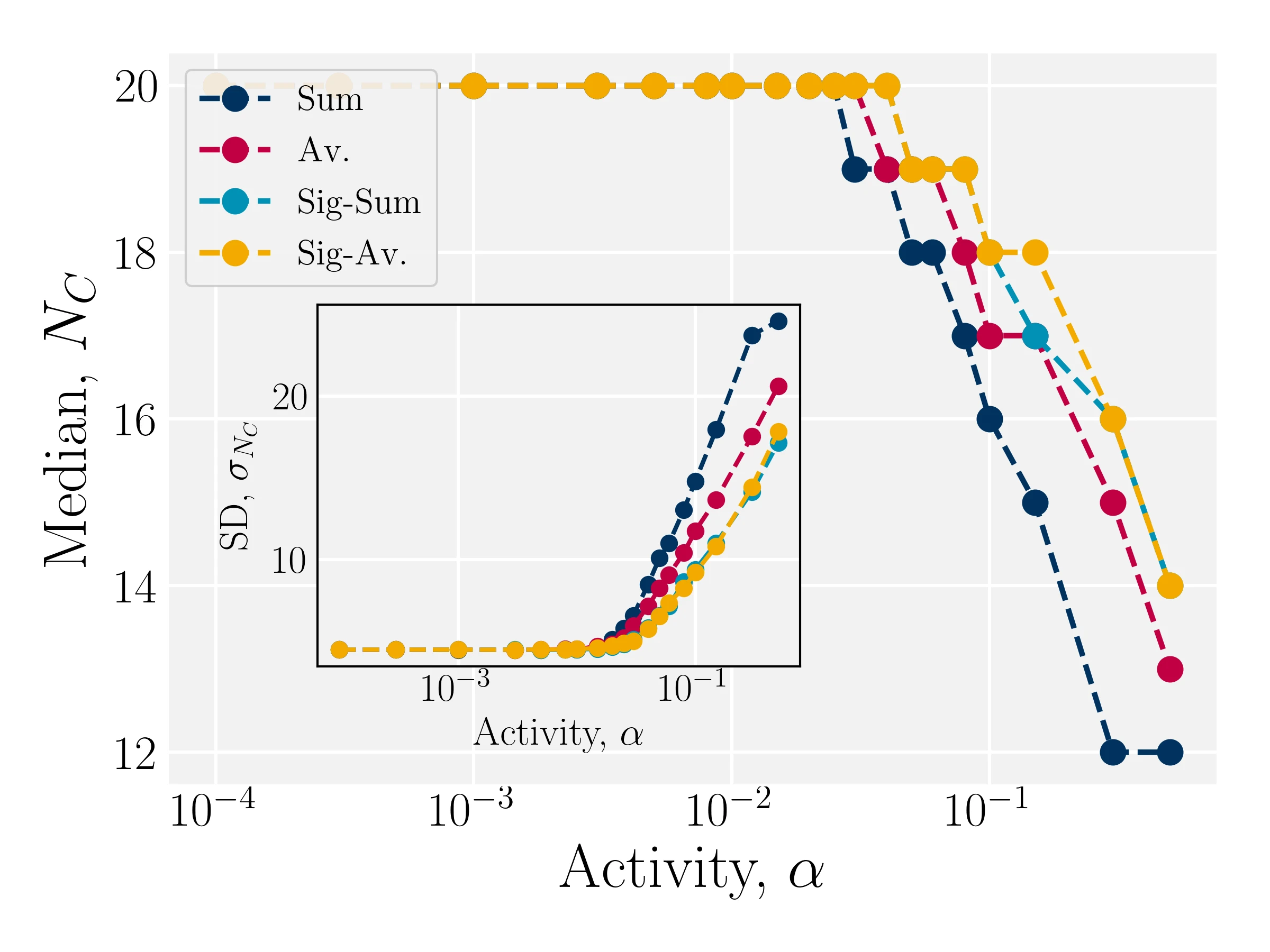
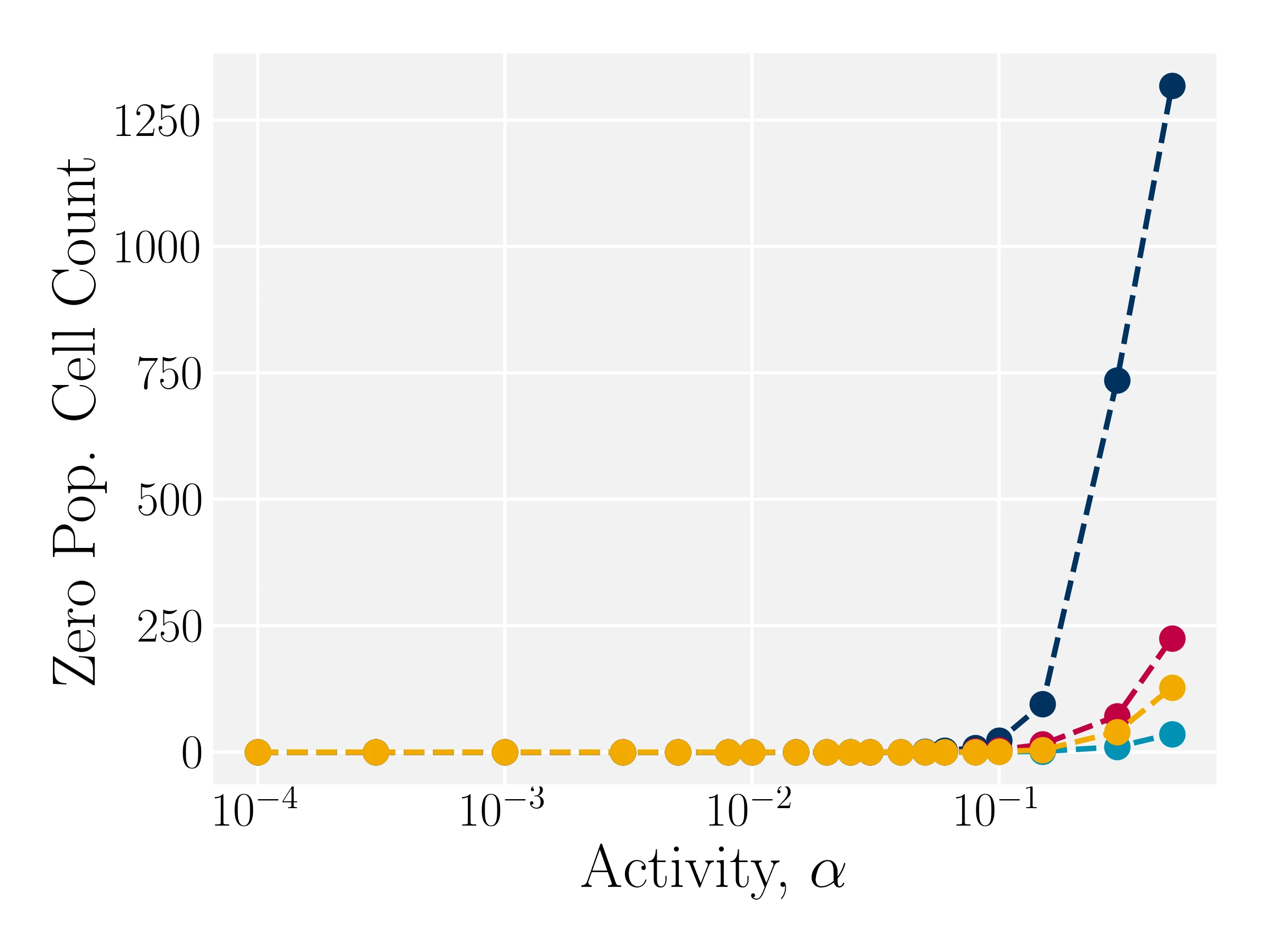
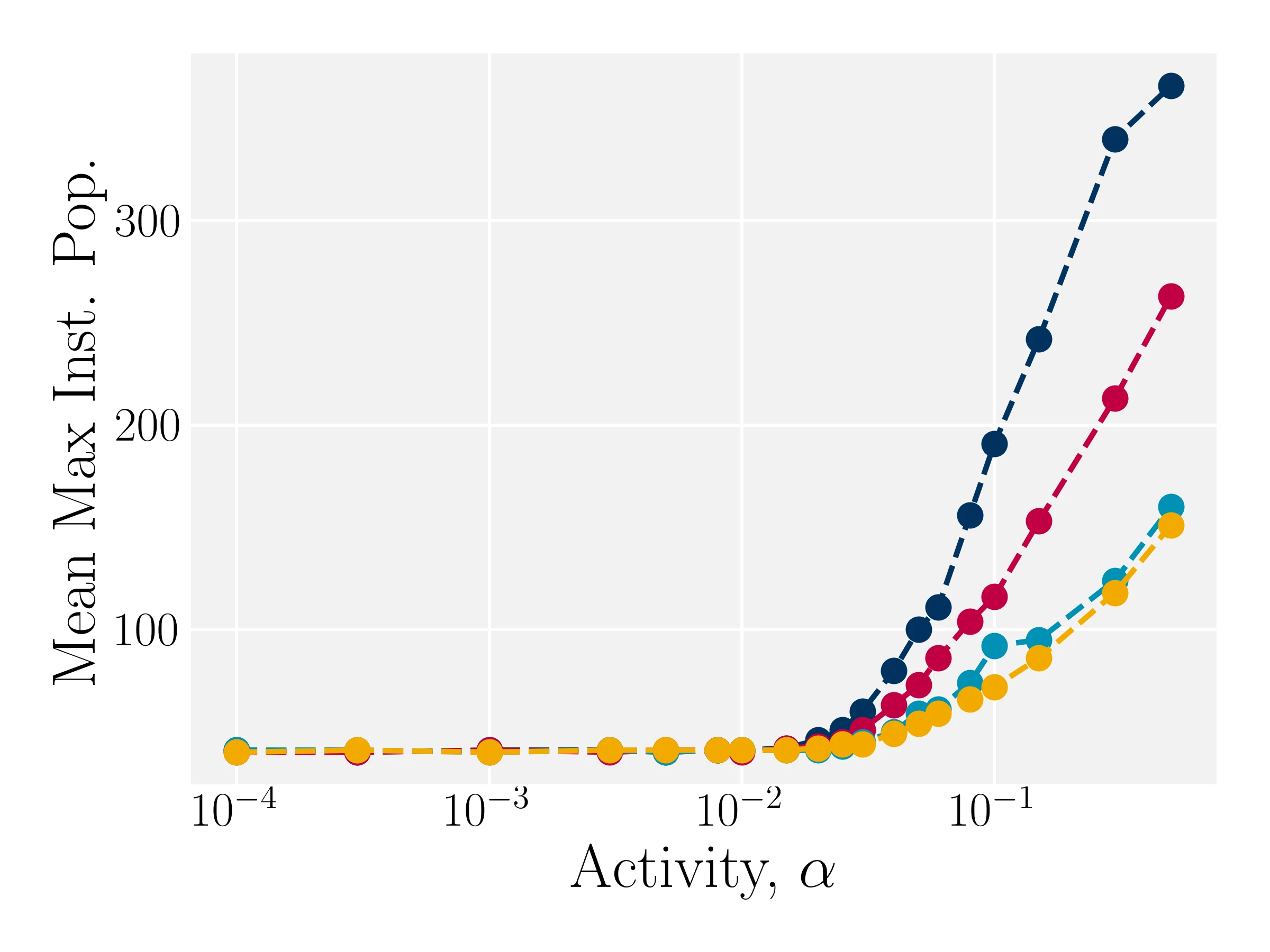
- Kozhukhov T, Loewe B, Shendruk T, in prep.
Modulations reduce density band width
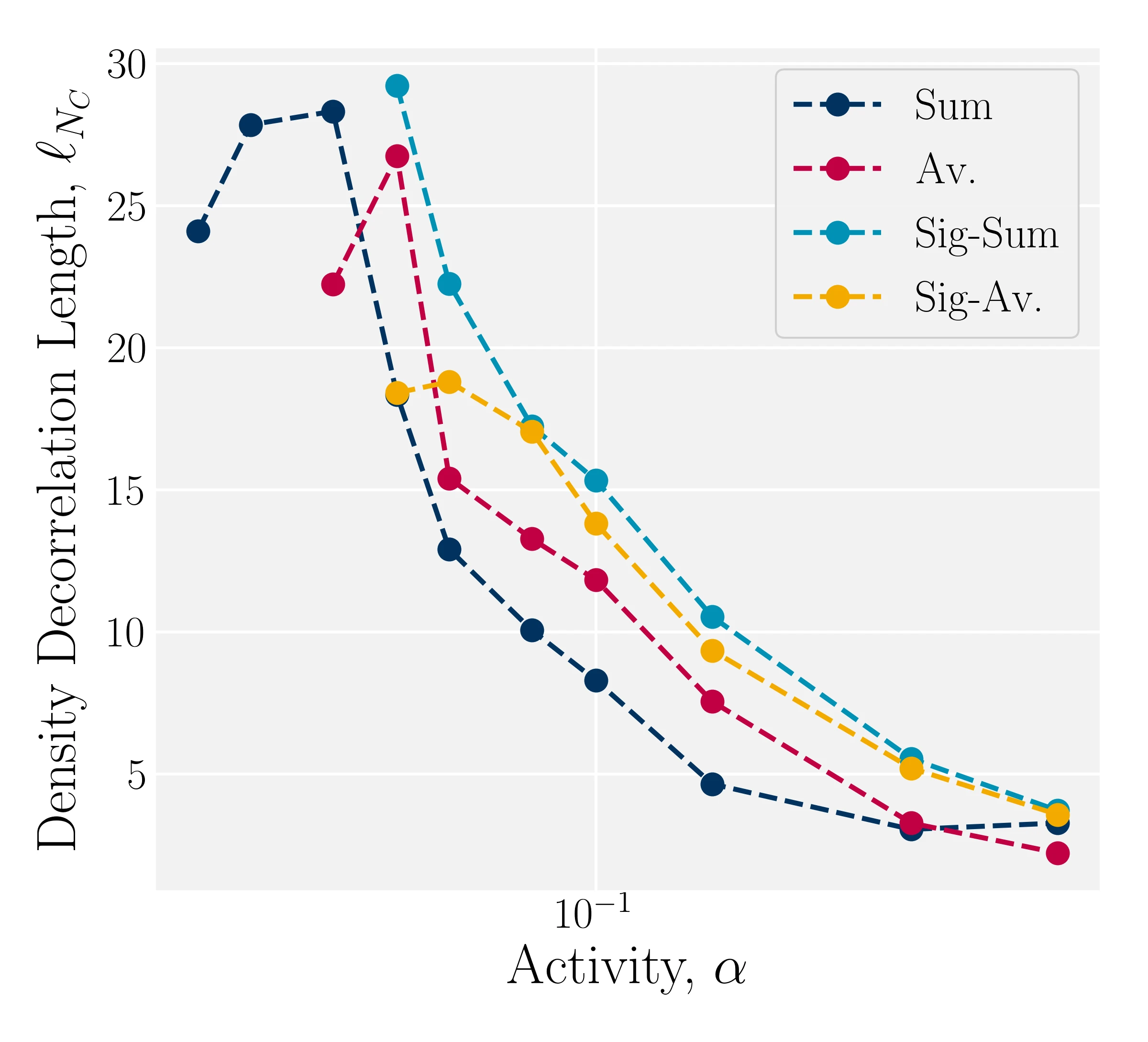

- Kozhukhov T, Loewe B, Shendruk T, in prep.
Modulations reduce density-induced drift
Fick's law: Density-induced drift $\propto \left| \nabla \rho \right|$
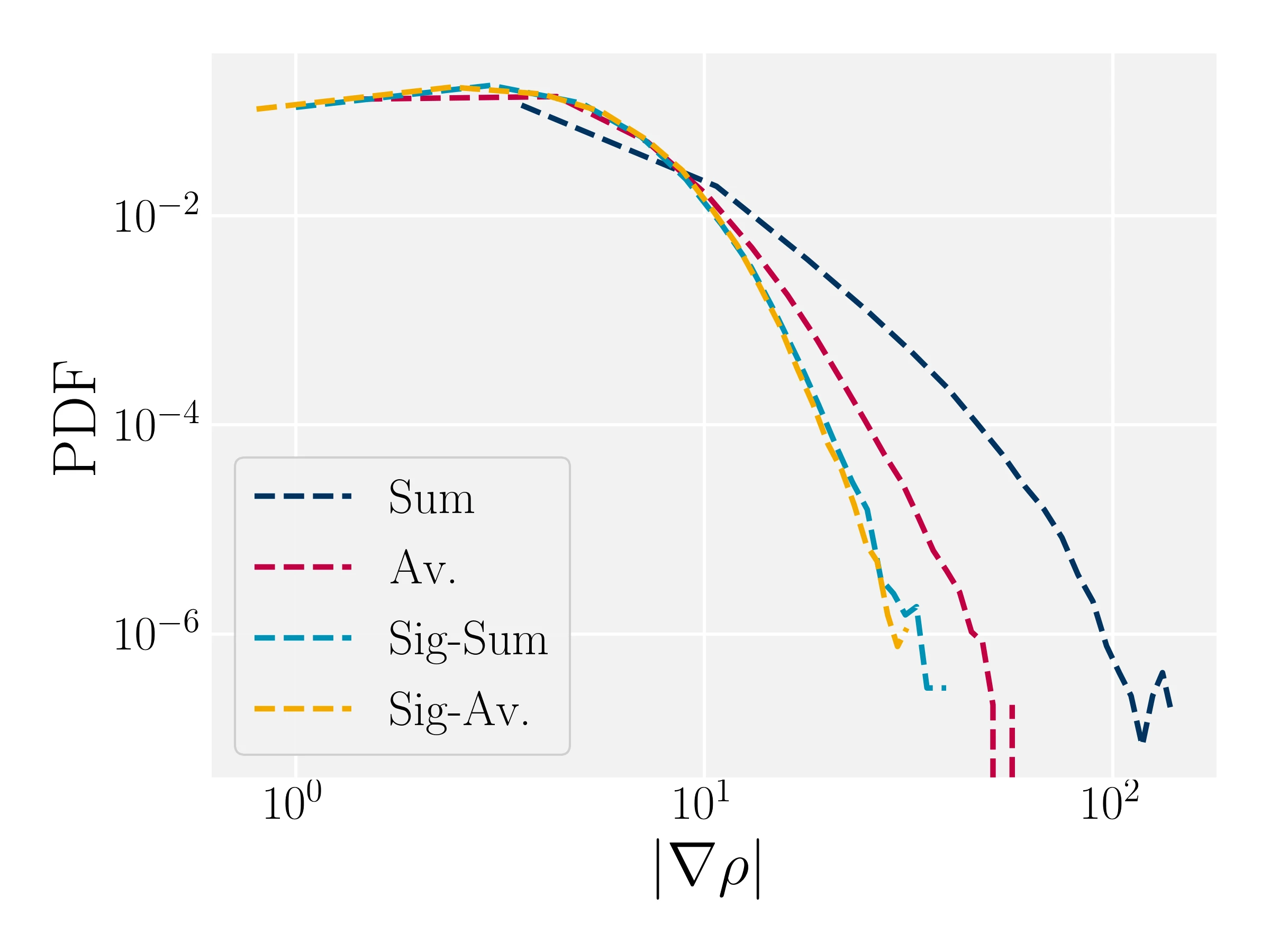
$\alpha=0.1$

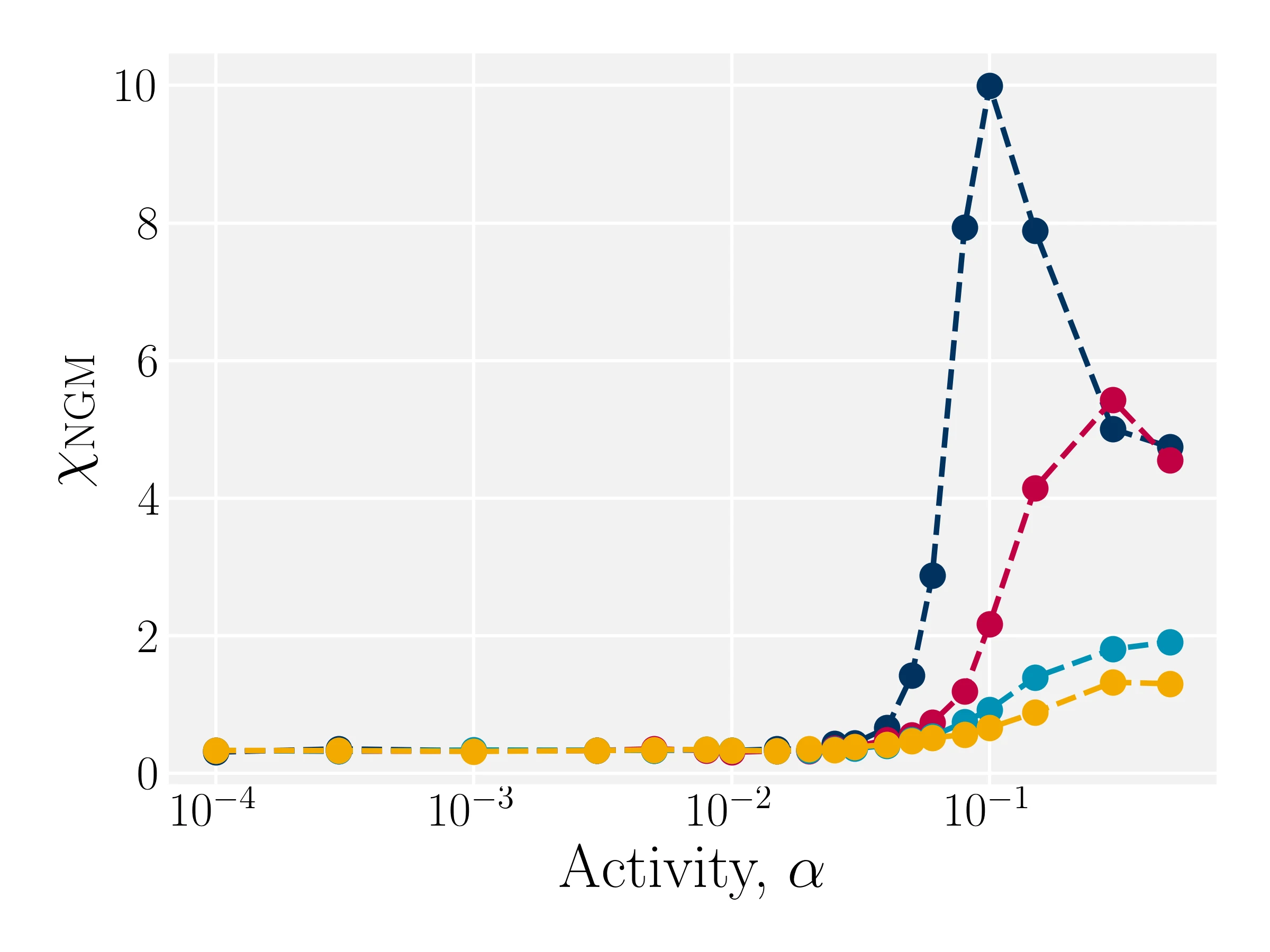
$\chi_\mathrm{NGM}=\frac{d}{d+2} \frac{\Delta r^4}{|\Delta r^2|^2}-1$
- Kozhukhov T, Loewe B, Shendruk T, in prep.
Giant number fluctuation analysis reveal algorithm regimes
_scalesCB-web.webp)

$\sigma_{N_C}=A\langle N_C \rangle^\nu$

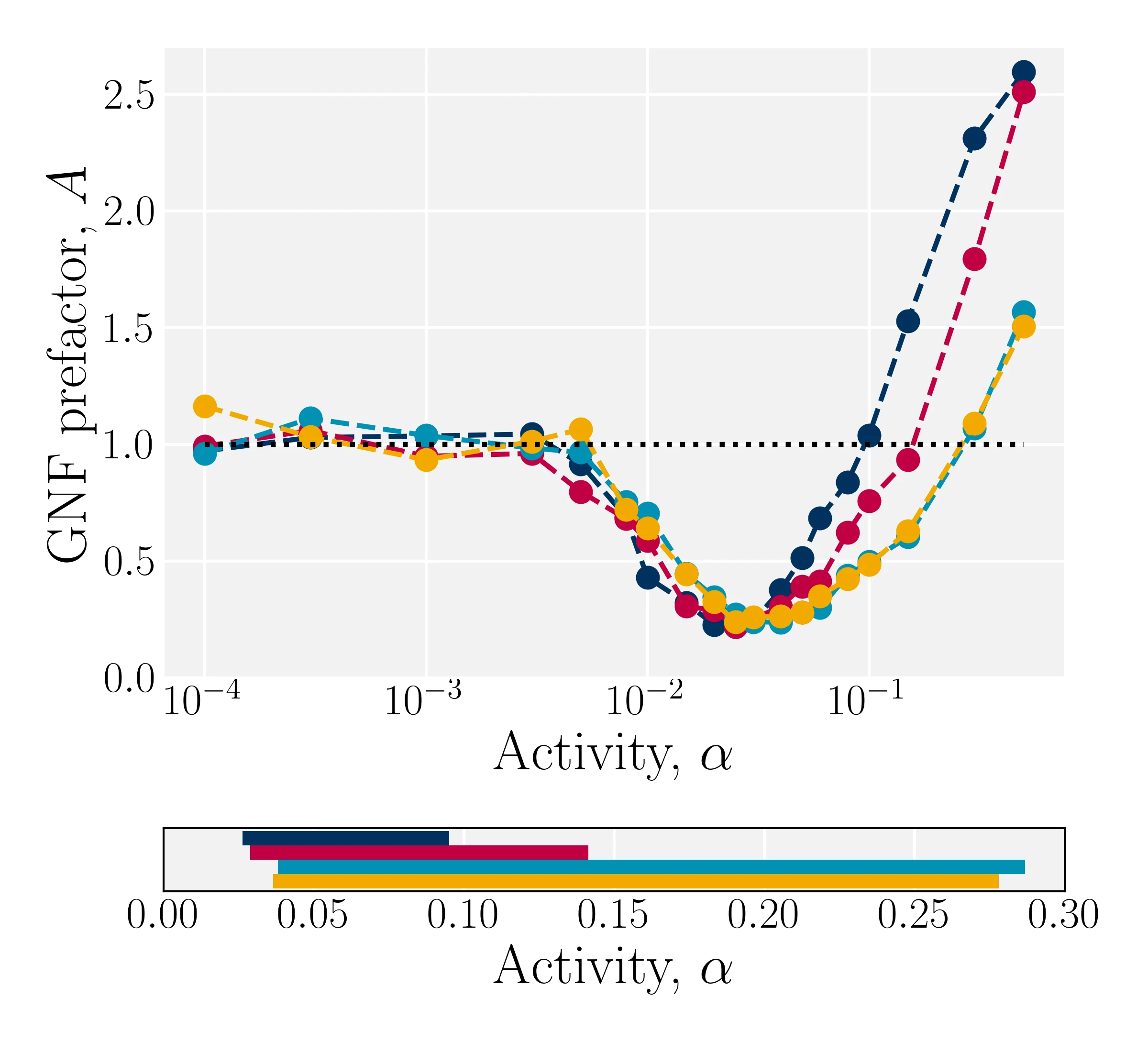
- Kozhukhov T, Loewe B, Shendruk T, in prep.
Table of contents
- Introduction & Motivation
- Mesoscopic simulation techniques &
Multi-Particle Collision Dynamics (MPCD) - Active Nematic (AN-) MPCD
- Modulated AN-MPCD
- Applications of AN-MPCD
- Conclusion
Applications of mesoscale AN-MPCD

Louise Head
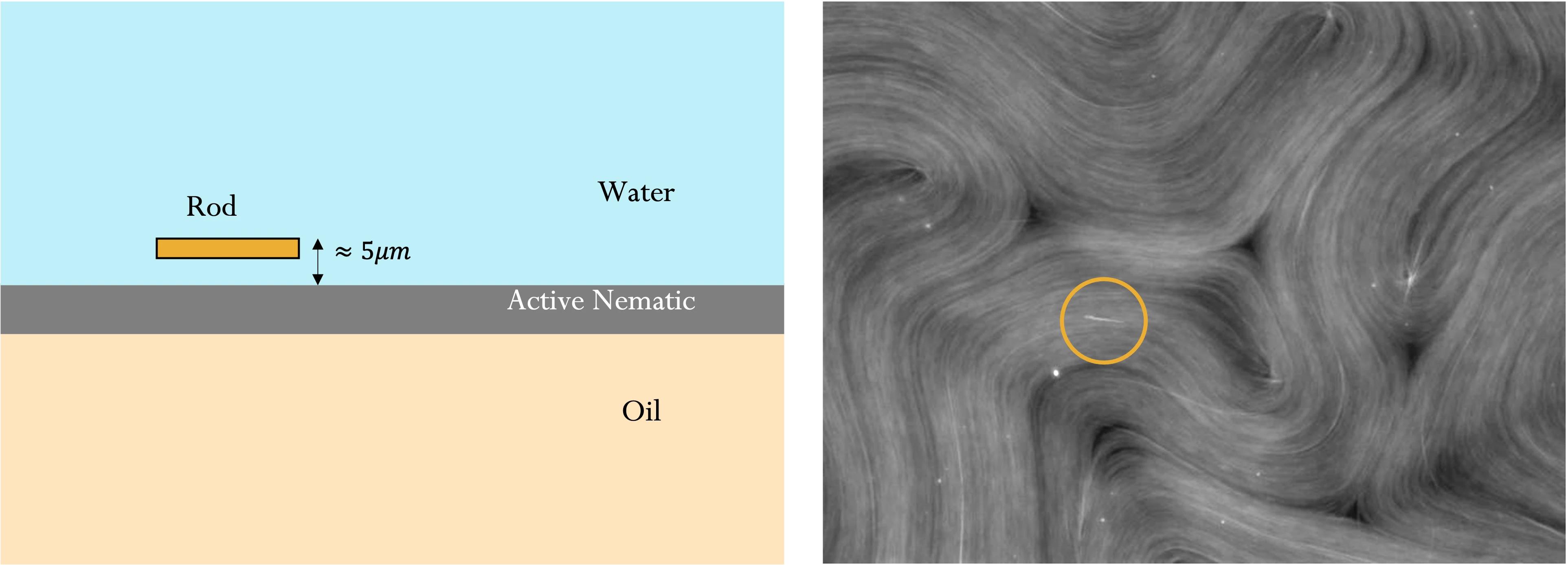
Active Av.
Applications of mesoscale AN-MPCD

Zahra Valei
Sigmoidal Sum
Applications of mesoscale AN-MPCD

Ryan Keogh

Active Av.
Keogh R, Kozhukhov T,et al., Submitted 2023
Applications of mesoscale AN-MPCD

Kira Koch

Mark Curtis-Rose
Applications of mesoscale AN-MPCD

Benjamín Loewe

Humberto Híjar
Applications of mesoscale AN-MPCD

Benjamín Loewe
Positive overcharge
Negative overcharge
Summary
-
A force dipole reproduces active turbulence for sufficient activity
- $\alpha > \alpha_\text{turb} \simeq 2.5\times 10^{-2}$
-
Density dependent activity modulation reduces density fluctuations
- Sigmoidal Av. for general use
- Sigmoidal Sum for minimising low density regions
- AN-MPCD provides a strong framework to simulate out of equilibrium mesoscale systems
t.shendruk@ed.ac.uk, t.kozhukhov@sms.ed.ac.uk

View these slides online at www.Kozhukhov.co.uk/
Acknowledgements













Appendix Slides
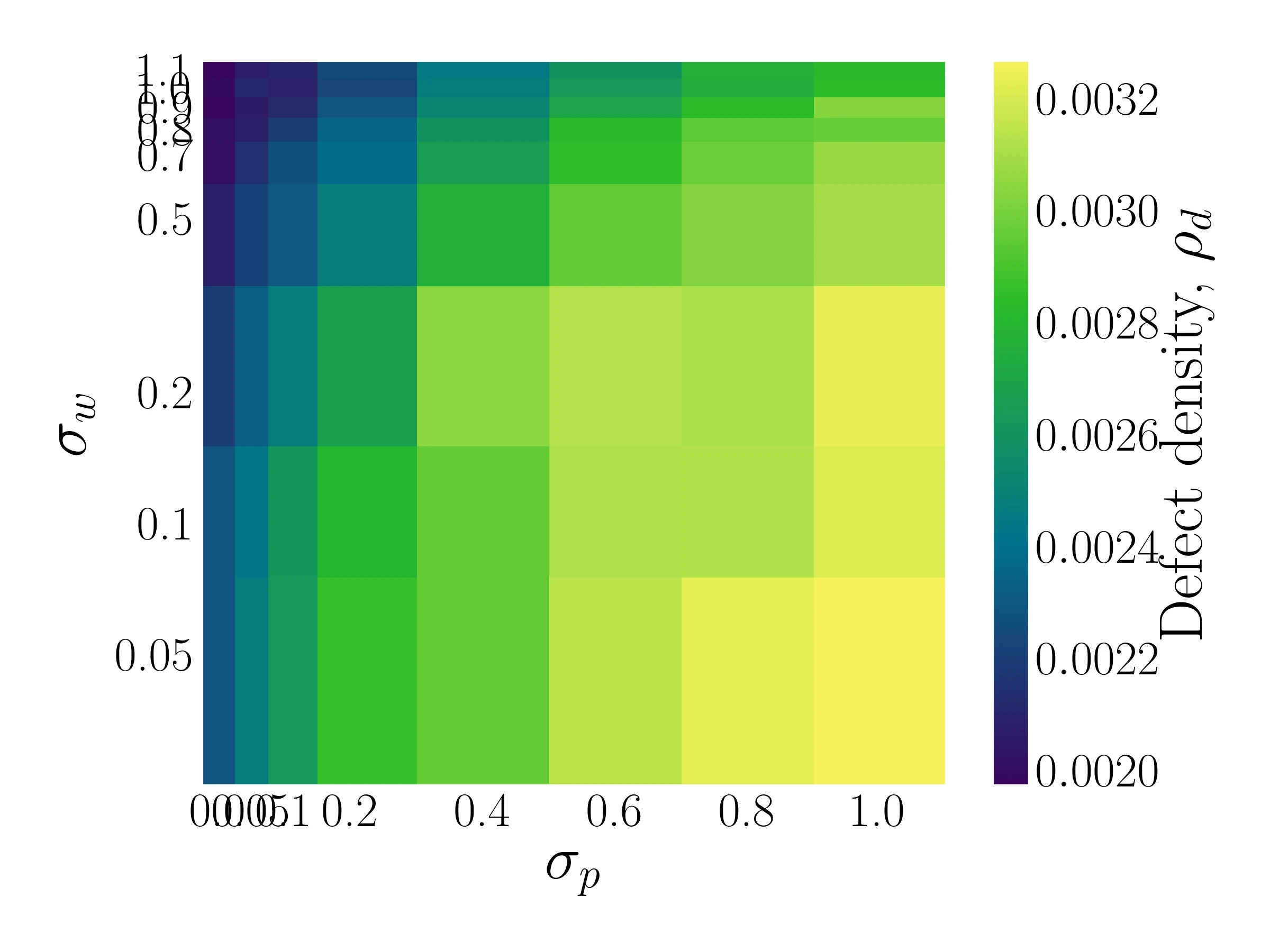

Chosen params are $\sigma_p=0.4, \sigma_w=0.5$